
Different Cases of Tangent Circles
By Paulo Tan
I investigated three
different constructions of a tangent circle to two given circles. The first case starts with one circle
inside the other. The second case
starts with two intersecting circles.
The last case starts with two disjoint circles. All three cases involve d very similar
constructions. I also looked at
the possible number of tangent circles in each case.
The construction of the first
case is a familiar one. Start with
circle C inside of circle A, pick a point of tangency on circle A (call this
point G), draw a line through point A and G, and draw a circle centered at
point G with the same radius as circle C. The next decision affects how the
tangent circle will behave.
We look for the intersection of line AG and circle G. There are two such intersections, point
F and point H (fig1). We initially
picked point F, constructed a segment from point C to point F, found the
midpoint of line segment CF, and constructed the perpendicular line to line
segment CF through the midpoint of line segment CF. Point E represents the
intersection of line AG and the perpendicular line to line segment CF. Thus,
point E represents the center of the tangent circle.
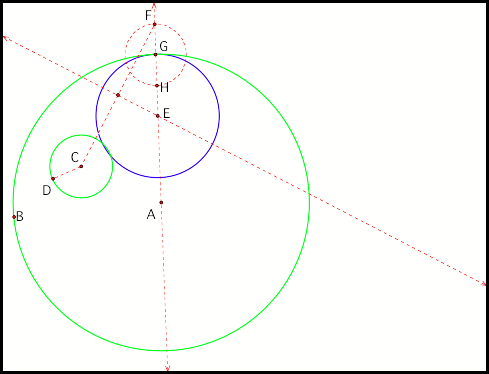
Fig1.
Suppose we chose point H instead
of point F as the intersection of line AG and circle G. The tangent circle now encircles circle
C (fig2). This tangent circle will
encircle circle C no matter where initial choice of point G lies on circle
A. The reason is that, in this
case, the locus of E is an ellipse that is always inside of circle A
(fig2b).
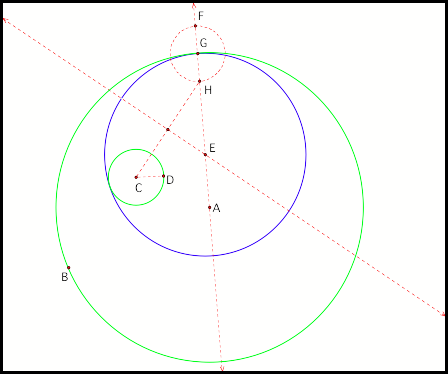
Fig2.
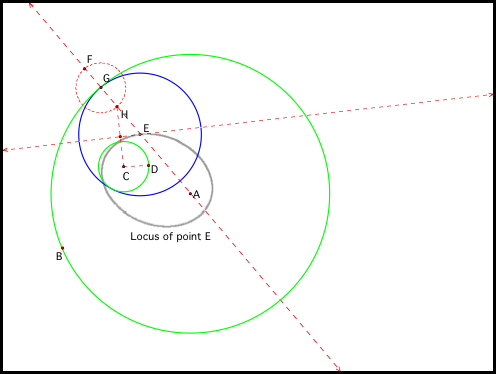
Fig2b.
Hence, in the case where we
are given one circle inside another, we could always construct two distinct
tangent circles.
The second construction starts
with circle C and circle A intersecting.
The construction is similar to the first case. Once again, the decision to connect point C to point H or F
gives two different types of tangent circles (fig3).
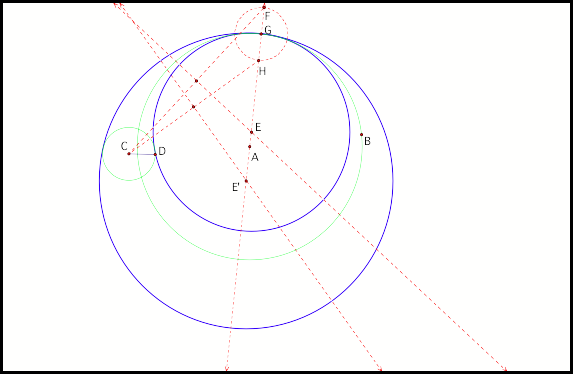
Fig3.
Joining point C to point H
produces tangent circle EÕ. Once
again this tangent circle appears to encircle circle C. However, if we were to choose our
initial point G closer to circle C, weÕll notice that this tangent circle no
longer encircles circle C. The
reason is that in this case where we start with two intersecting circles, it is
now possible for line m and line p to be perpendicular. As a result lines m and n are parallel
(fig4). Remember line n represents the line through the center of circle A and
point G (the point of tangency).
Line m is the perpendicular bisector of line CH. Thus, when the initial point of
tangency is chosen such that line n is parallel to line m, then tangent circle
EÕ cannot exist.
On the other hand line p and
line n could never parallel in this case. Therefore, tangent circle E always exists in the case of two
intersecting circles.
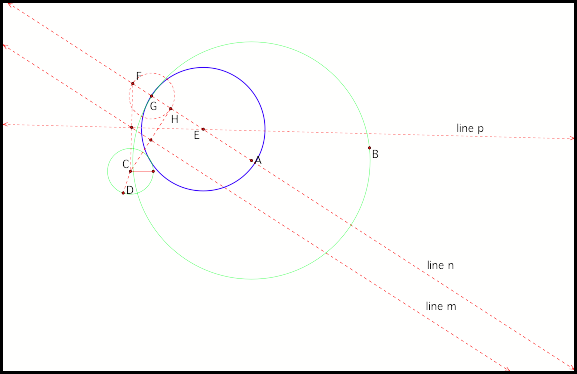
Fig4
Also when the intersection of
line m and line n is outside of circle A, then tangent circle EÕ will not
encircle circle C (fig5).
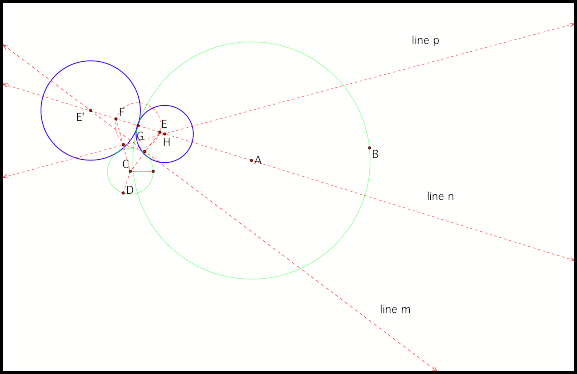
Fig5.
The intersection points of
circle A and circle C also provide some additional insight. At these intersection points tangent
circle E and EÕ are the same. More
specifically they are the same point.
Thus, in the case where two
intersecting circles are given, we can hypothesize:
1. It is not always possible to construct two distinct
tangent circles.
2. Circle EÕ may not always exist.
3. There are two points where E and EÕ are the same.
Next letÕs look at the locus
of E and EÕ(fig5b).
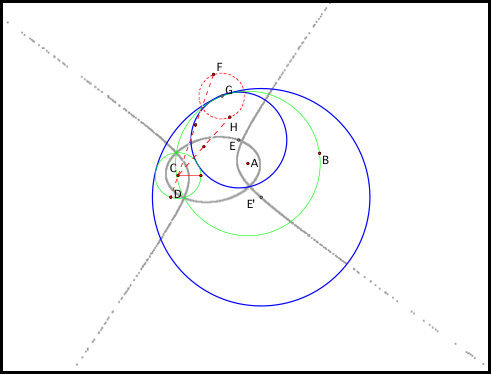
Fig5b.
The locus of E and EÕ confirms
our hypothesis in the case of two intersecting circles. The locus of E is again an ellipse,
which means that tangent circle E will always exist. The locus of EÕ, on the other hand, is a hyperbola. This confirms that it is possible for
circle tangent EÕ to not exist. In
addition, the two intersections of circle A and circle C coincides with the
intersections of locus E and EÕ.
These intersections represent the two points where tangent circle E and
EÕ are the same.
Lastly, when we construct the
tangent circle of two disjoint circles.
The construction is similar to the first two cases and we could once
again have two possible tangent circles (fig6).
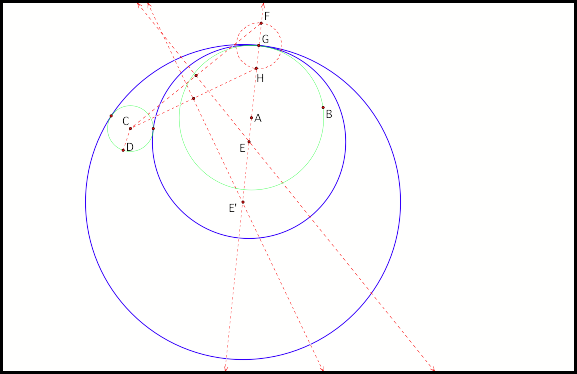
Fig6.
As with the previous case the
intersection of line m and n could be outside of circle A, which implies
tangent circle EÕ will not always encircle circle C. Also line m and n could still be parallel. Unlike the previous case, however, it
is possible for line n and line p to also be parallel (fig7).
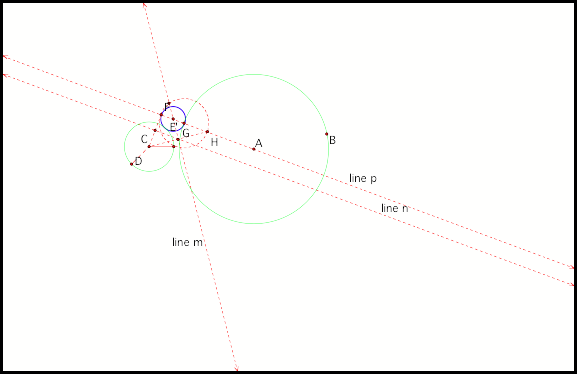
Fig7.
So, when line n and line p
are parallel tangent circle E does not exist.
Thus, in the case where two
disjoint circles are given we hypothesize:
1. It is not always possible to construct two distinct
tangent circles.
2. Tangent circle E and tangent circle EÕ may not exist
in certain situations.
3. It is not possible for E and EÕ to be the same.
Once again, weÕll investigate
the locus in the case of two disjoint circles (fig7b).
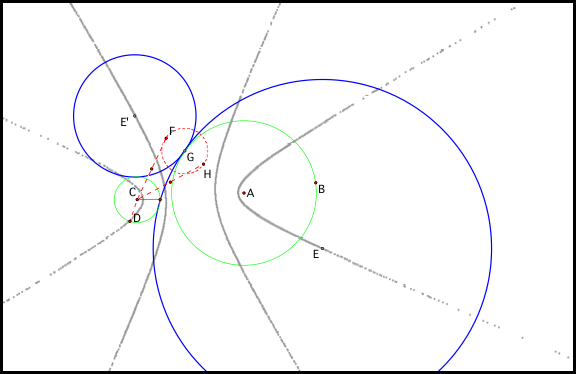
Fig7b.
This time the locus E and EÕ
both form a hyperbola. Hence, our hypothesis
is correct that both tangent circle E and EÕ do not exist at certain
locations. Also, since the
hyperbolas donÕt intersect it is not possible for tangent circle E and EÕ to be
the same.