_______________________________________________________________________________________________________

Cryptorithms

Presented by:

Dana TeCroney

Cryptorithms are puzzles where a single digit number replaces every letter, and the challenge is to find the corresponding numbers. For example:

These puzzles test your knowledge of addition properties (or other arithmetic operations), often with a not so hidden message…

One way to solve this problem is to begin with the left most digit in the answer. In this case, L = 1 because the most that could be grouped (when the digits in a column sum to 10 or more) from the ten thousands column (the B column) is 1. At this step, you can also conclude that B = 9 and O = 0.

Consider:

If E + C were the next two larges available digits, 8 + 7 = 16, and if we add 2 (the largest number that could be grouped from a previous column) then the sum is 18 < 20, which means B = 9 to produce L = 1. Furthermore, O = 0.

Now lets fill in our progress (notice I put in the group from the thousands column):

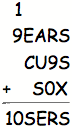
B = 1; L = 1; O = 0

At this point, the problem gets interesting because the solution is not unique (yes, sometimes there is more than one possible answer!). There are a lot of S’s in the problem, so that might be a good place to go next. Lets look at some different possibilities for the one’s column and keep in mind, S + S + X = S, so S + X = 10.

Try I: S = 7; X = 3

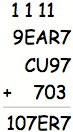
If this were the case, the E + C must be 16 in order to add a group of 10 to the ten thousands place (the 9 and 1). This can’t happen though because the largest two available numbers are 8 and 6, 8 + 6 = 14. Even if one were added to this, we still couldn’t get 16…

Try II: S = 6; X =4

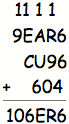
Here, E + C > 10 because earlier we showed that a group of 10 went with the 9. In fact E + C = 15. If E = 8, the A + U = 10, but this can’t happen because the available digits would be 5, 3, and 2, no two of which sum to ten. So what if E = 7? Again this won’t work for similar reasons.

Try III: S = 2; X = 8

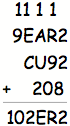
In this case, E + C = 11. Let’s try E = 4 and C = 7. This implies that A + U = 11. One possibility is A = 5 and U = 6, leaving R = 4.

B = 9 C = 7 S = 2 L = 1

E = 4 U = 6 O = 0 O = 0

A = 5 B = 9 X = 8 S = 2

R = 4 S = 2 S = 2 E = 4

S = 2 R = 4

S = 2

Here is one answer, can you find any more???

If you would like to try some cryptorithms, press here.

Possible extensions:

Finding more answers. On the linked page, there are crytorithms using different operations, and these could be explored. These could be used in a classroom as an introduction to logic that may interest students. There are many conditional situations that result in these problems and force students to consider a number of different cases.