Exploring Loci of Parabolas

By

Princess Browne

We will look at the graph of y = ax² + bx + c

(b is varied and a and c are held constant)

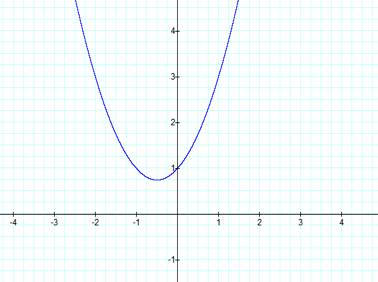
First, we will graph the equation where a, b, and c are equal to 1.

Like any parabola the graph is concave upward when a is positive. Therefore the graph will be concave downward when a is negative. Because c = 1 the graph is not symmetrical around the y-axis. The parabola passes through the points (0.1) because c = 1. When x = 0, the graph would be symmetrical around the y-axis. Next, we will graph the equation where b is varied and a and c remain 1.

Yellow

Purple

Red

Blue

Green

Teal

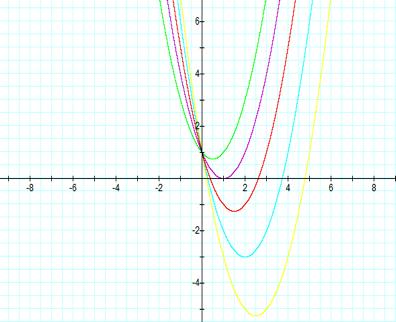
The following graphs intersect the y-axis at (0,1) because c = 1. The vertex is always left of the graph when b is greater than 0. When b = 0 the vertex is on the x-axis. The real root of the equation occurs where the parabola intersects the x-axis. The graph of y = x² + 2x + 1 have a real root because it intersect the x-axis. The graph of y = x² + 1x + 1 does not have any real root because it does not intersect the x-axis. When b is positive the real roots occur on the negative side of the y-axis.

Green

Purple

Red

Teal

Yellow

When b is negative the graphs intersect the y-axis at (o,1). The vertex is to the right of the graph and the vertex is on the y-axis when b = 0. The graph have no real root when b = -1.

Purple y = x² + 4x + 2

Red y = 2x² + 4x + 2

Blue y = 3x² + 4x + 2

Green y = - x² + 4x + 2

Teal y = -2x² + 4x + 2

Yellow y = -3x² + 4x + 2

From the picture above, we can conclude that each parabola passes through the point (0,2). When a is positive the parabola is concave up and the parabola is concave down when a is negative. The x-coordinate of the vertex is x = -b/2a.

Return