Parametric Equations

Karyn Carson

For various a and b, investigate

Let’s set a and b equal to a range of values and see what happens and what relationships can be seen…

Let’s begin with situations where a = b and they equal one:

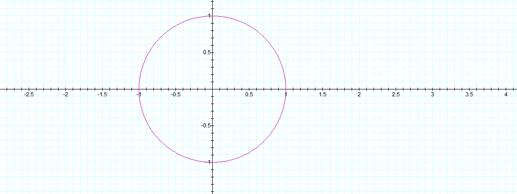
This equation results in a circle with center at the origin and a radius of one.

Now, let’s change a and b to 2:

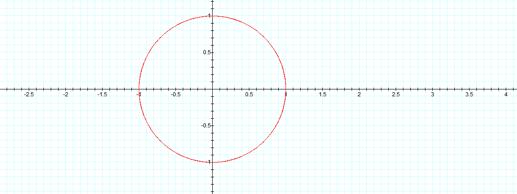
It’s the same circle. How can that be?

Let’s change a and b to 3:

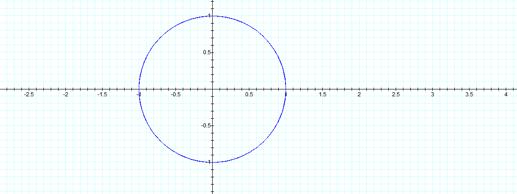
Same circle…

What happens if we make a and b less than one? How about 0.5?

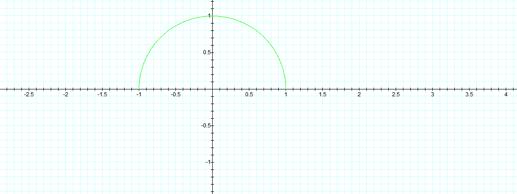
Aha! We get a half-circle! I think this means that if a and b are more than one then the same points are graphed, thereby just going over the previous points.

What if a and b are different?

a=1 and b=2

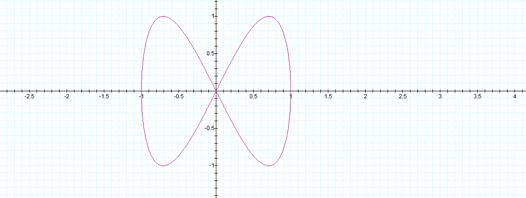
This is a much different graph! The limits are still one, but now it looks like a bow…What will happen if a=1 and b=3?

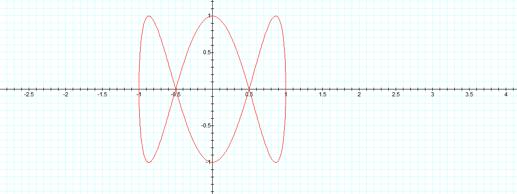
Does b determine the number of sections if a and b aren’t equal?

a=1, b=4

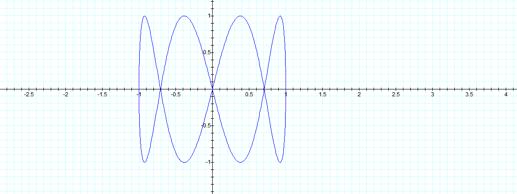
It would appear so…at least when a=1. Now I’d like to keep b constant and vary a…

a=2, b=1

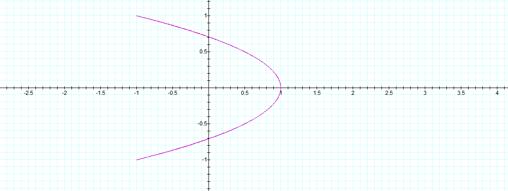
The limit appears still to be one. I need to look at more graphs…

a=3, b=1

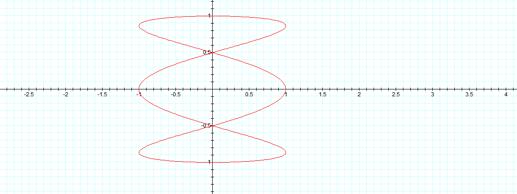
This looks just like the graph where a=1 and b=3, but it’s been turned and visually appears to be centered on the y-axis as opposed to the other graph, which appeared to be centered on the x-axis. Now a seems to be determining the number of sections.

Back to Karyn’s Homepage