Quadratic Function

y = x² + bx + 1

(varying ‘b’)

Karyn Carson

Let’s start by looking at the graphs of the function y = x² + bx + 1, and vary b from

-3 to 3:

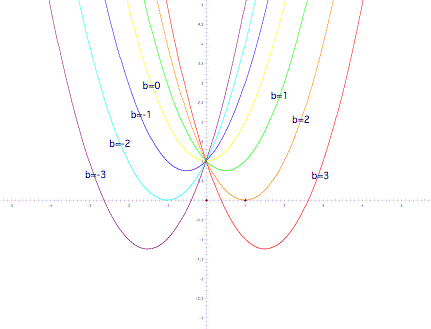
What I’d like to look at is the vertices of each of the parabolas. To figure these out, I’ll use the vertex formula 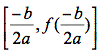and an Excel spreadsheet:

b	x-coordinate	y-coordinate
-3	1.5	-1.25
-2	1	0
-1	0.5	0.75
0	0	1
1	-0.5	0.75
2	-1	0
3	-1.5	-1.25

And now, let’s plot these points on the graphs of the other functions:

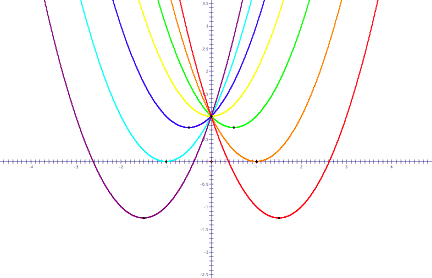
It seems as though a pattern is formed – the vertices of the parabolas look like they form another parabola! If we ‘connect the dots’, we do get a parabola:

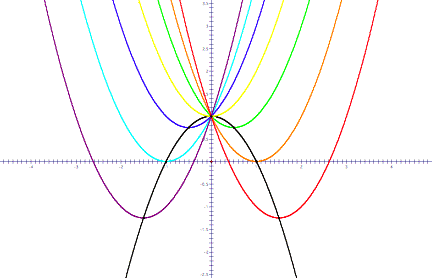
This parabola is a reflection of the graph of x² +1, so it’s equation must be y = -x² +1. If we plug the x-values from the vertices into the equation, we can see that the points do fit the equation.

x-coordinate
1.5	-1.25
1	0
0.5	0.75
0	1
-0.5	0.75
-1	0
-1.5	-1.25

Back to Karyn’s Homepage