|
Michelle E. Chung |
*
EMAT6680 Assignment 1: Graphing Functions and Relations |
|
6. Graph
 . .
What do you expect for the graph of 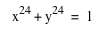 or or 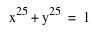 ? ?
|
 |
Before thinking about the graphs of 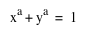 , ,
let's seperate these into two different
cases, which is when n is an even number and when n is an
odd number.
|
| The graphs of
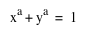
when a is ODD |
|
|
When a=1:

- The graph is a straight line because x+y=1 is same as y= -x+1.
- The graph of x+y=1 is a straight line that its slope is -1 and its y-intercept is 1.
When a=3:

- The graph is NOT a straight line.
- It looks like a top of a hat, and the coordinates of the top of the hat is (0.793701, 0.793701).
Also, it is symmetric to y=x.
When a=5:

- The graph is NOT a straight line, either.
- It looks like a top of a hat, too, but the coordinates of the top of the hat is (0.870551, 0.870551).
It is symmetric to y=x, too.
When a=7:

- The graph is NOT a straight line, either.
- It looks like a top of a hat, too, but the coordinates of the top of the hat is (0.905724, 0.905724).
It is symmetric to y=x, too.
When a=9:

- The graph is NOT a straight line, either.
- It looks like a top of a hat, too, but the coordinates of the top of the hat is (0.925875, 0.925875).
It is symmetric to y=x, too.
|
Conclusion
|
- As you see, the graph of
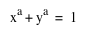 when a is odd is a straight line with a curve part, which looks like a top of a hat, except when a=1(it is a straight line). when a is odd is a straight line with a curve part, which looks like a top of a hat, except when a=1(it is a straight line).
- It is symmetric to y=x.
- The curve part is getting pointier when the value of a is greater, and we actually can notice that the coordinates of the top of it is getting greater.
|
Back to the Top |
|
The graphs of
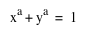
when n is EVEN |
|
|
When a=2:
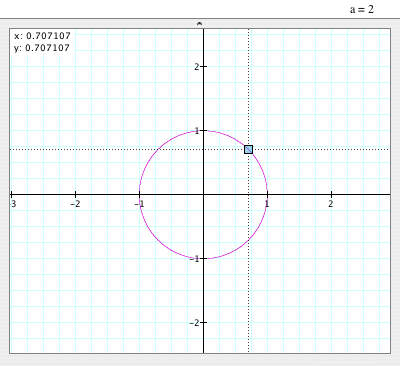
- The graph is a circle that its center is (0,0) and its radius is 1 because it is a equation of a circle.
- It is also symmetric to y=x because (0.707107, 0.707107) is on the circle.
When a=4:
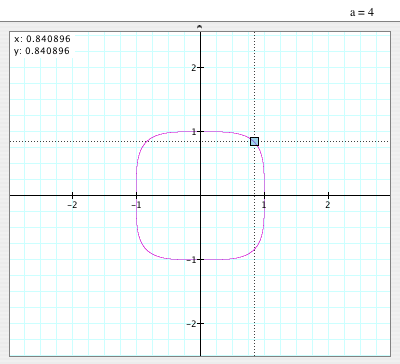
- The graph is NOT a circle anymore.
- It looks like a square with some curve corners, or it looks like a flatted circle
that has (0,0) as its center and radius 1, too, but one of
the coordinates of the corner is (0.840896, 0.840896).
- It is also symmetric to y=x, too.
When a=6:
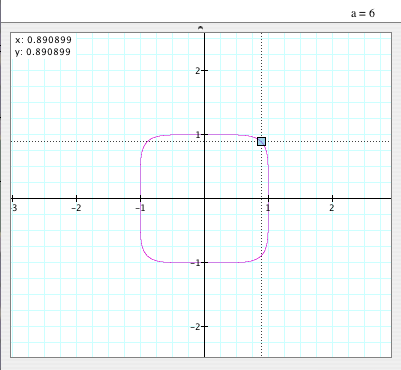
- The graph is NOT a circle anymore, either.
- It looks like a square with some curve corners, or it looks like a flatted circle
that has (0,0) as its center and radius 1, too, but one of
the coordinates of the corner is (0.890899, 0.890899).
- It is also symmetric to y=x, too.
When a=8:
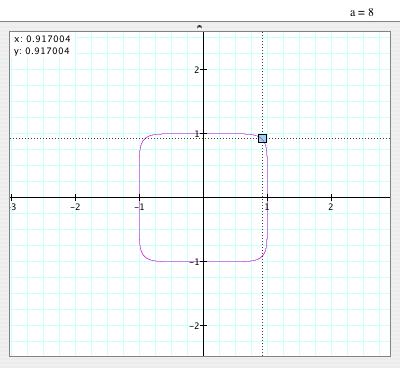
- The graph is NOT a circle anymore, either.
- It looks like a square with some curve corners, or it looks like a flatted circle
that has (0,0) as its center and radius 1, but one of the
coordinates of the corner is (0.917004, 0.917004).
- It is also symmetric to y=x, too.
When a=10:
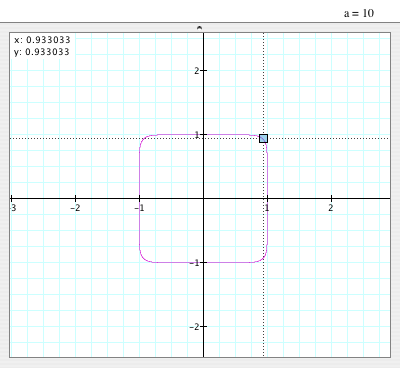
- The graph is NOT a circle anymore, either.
- It looks like a square with some curve corners, or it looks like a flatted circle
that has (0,0) as its center and radius 1, too, but one of
the coordinates of the corner is (0.933033, 0.933033).
- It is also symmetric to y=x, too.
|
Conclusion
|
- As you see, the graph of
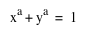 when a is even is a flatted circle that has (0,0) as its center and radius 1, except when a=2(it is a circle). when a is even is a flatted circle that has (0,0) as its center and radius 1, except when a=2(it is a circle).
- It is symmetric to y=x.
- The corners of the flatted circle are getting pointier when the value of a is
greater, and we actually can notice that the coordinates of the
top of
it are getting greater.
|
Back to the Top |
* The graph of 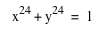
|
Guess on the graph of
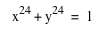
|
|
|
Because the graph of 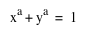 when a is even is a flatted circle, the graph of when a is even is a flatted circle, the graph of 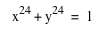 would be also a flatted circle with (0,0) as its center and radius 1; however, its corners would be pointer than others we saw previously because its value of a is greater than them. Also, it would be symmetric to y=x. would be also a flatted circle with (0,0) as its center and radius 1; however, its corners would be pointer than others we saw previously because its value of a is greater than them. Also, it would be symmetric to y=x.
|
The graph of
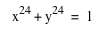
|
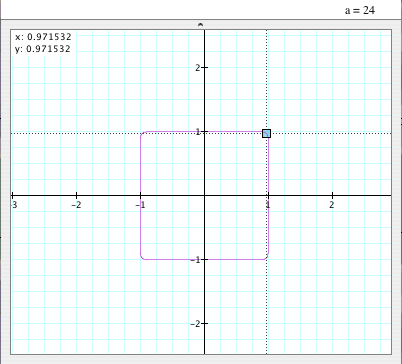
- As you see, it IS a flatted circle with (0,0) as its center and radius 1.
- Its corners are pointer than others, and one of the coordinates is (0.971532, 0.971532).
- It is also symmetric to y=x.
|
Back to the Top |
* The graph of 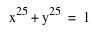
| Guess on the graph of
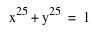
|
|
|
Because the graph of 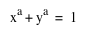 when a is odd is a straight line with a curve part, which looks like a top of a hat, the graph of when a is odd is a straight line with a curve part, which looks like a top of a hat, the graph of 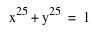 would be also a straight line with a curve part, which looks like a top of a hat; however, the top of the hat would be pointer than others we saw previously because its value of a is greater than them. Also, it would be symmetric to y=x. would be also a straight line with a curve part, which looks like a top of a hat; however, the top of the hat would be pointer than others we saw previously because its value of a is greater than them. Also, it would be symmetric to y=x.
|
The graph of
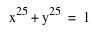
|

- As you see, it IS a straight line with a curve part, which looks like a top of a hat.
- The top of the hat is pointer than others, and the coordinates of it are (0.972655, 0.972655).
- It is also symmetric to y=x.
|
Back to the Top |
|
|
 Go Back to Top Go Back to Top |
 Go
Back to Michelle's Main page
Go
Back to Michelle's Main page |
 Go
Back to EMAT 6680 Homepage
Go
Back to EMAT 6680 Homepage |
Copyright
@ Michelle E. Chung |
 .
.![]() or
or ![]() ?
?![]() ,
,











