Michelle E. Chung

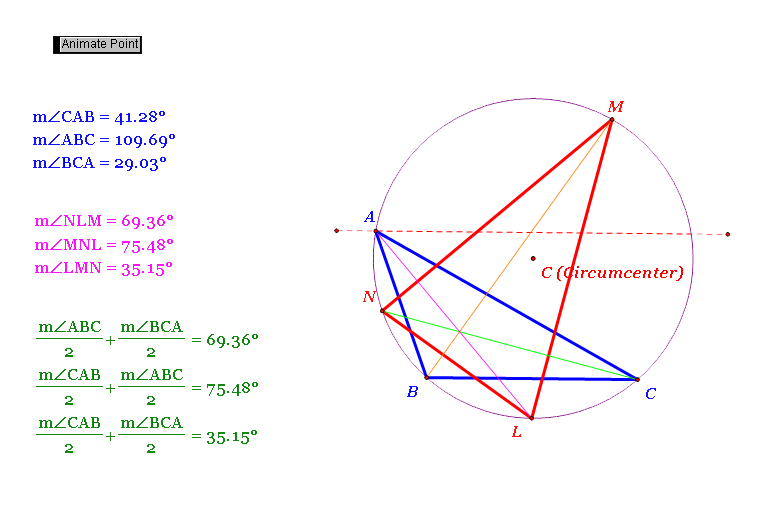
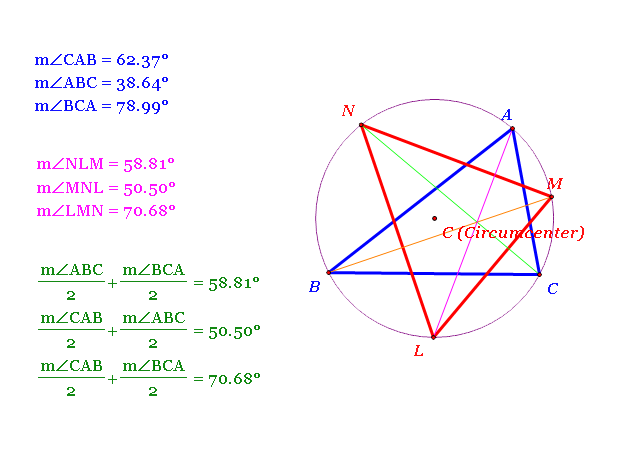
Look at the construction above.

Note that an angle of circumference of an arc is always constant.
From this fact, we can conclude following:

Angle L

Since angle ALM and angle ABM are angles of circumference of arc AM, m(angle ALM) = m(angle ABM).
Also, m(angle ABM) = m(angle ABC)/2 because line segment BM is an angle bisector.
So, m(angle ALM) = m(angle ABC)/2.

Similarly, m(angle ALN) = m(angle BCA)/2 because angle ALN and angle ACN are angles of circumference of arc AN and m(angle ACN) = m(angle BCA)/2.

Since m(angle NLM) = m(angle ALM) + m(angle ALN), m(angle NLM) = m(angle ABC)/2 + m(angle BCA)/2.

Angle N

Since angle CNL and angle CAL are angles of circumference of arc CL, m(angle CNL) = m(angle CAL).
Also, m(angle CAL) = m(angle CAB)/2 because line segment AL is an angle bisector.
So, m(angle CNL) = m(angle CAB)/2.

Similarly, m(angle CNM) = m(angle CBA)/2 because angle CNM and angle CBM are angles of circumference of arc CM and m(angle CBM) = m(angle ABC)/2.

Since m(angle MNL) = m(angle CNL) + m(angle CNM), m(angle MNL) = m(angle CAB)/2 + m(angle ABC)/2.

Angle M

Since angle BMN and angle BCN are angles of circumference of arc BN, m(angle BMN) = m(angle BCN).
Also, m(angle BCN) = m(angle BCA)/2 because line segment CN is an angle bisector.
So, m(angle BMN) = m(angle BCA)/2.

Similarly, m(angle BML) = m(angle BAC)/2 because angle BML and angle BAL are angles of circumference of arc BL and m(angle BAL) = m(angle BAC)/2.

Since m(angle LMN) = m(angle BMN) + m(angle BML), m(angle LMN) = m(angle BCA)/2 + m(angle BAC)/2.

Therefore, we can write angles of triangle LMN in terms of angles A, B, and C, and

m(angle L) = m(angle B)/2 + m(angle C)/2
m(angle N) = m(angle A)/2 + m(angle B)/2
m(angle M) = m(angle A)/2 + m(angle C)/2.

In addition, these facts hold for any triangle, and we can prove this fact by using GSP.

Acute Triangle
Right Triangle
Obtuse Triangle

Please check the GSP movie below.

Internal Angle Bisector Movie