Logo

 Michelle E. Chung
* EMAT6680 Final Assignment B: Ceva's Theorem

Proof of Ceva's Theorem
(P is outside)

Consider any triangle ABC.
Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in point D, E, and F respectively.

  • Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
  • Conjecture? Prove it!
  • Discuss how this theorem could be used for proving concurrency of the medians.
    Concurrency of other special points?
  • Explore a generalization of the result (using lines rather than segments to construct ABC) so that point P can be outside the triangle.


1. Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

Construction 1

: when point P is inside the triangle

    
1. When triangle ABC is an OBTUSE triangle

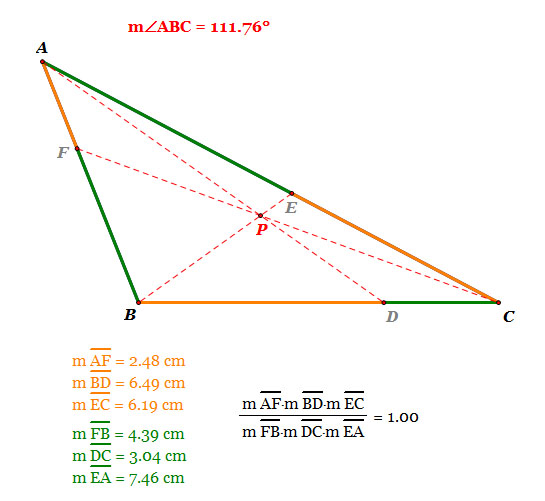
ObtuseTri_ratio

  • As we see, when the triangle ABC is an obtuse triangle, the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) is 1.
2. When triangle ABC is a RIGHT triangle

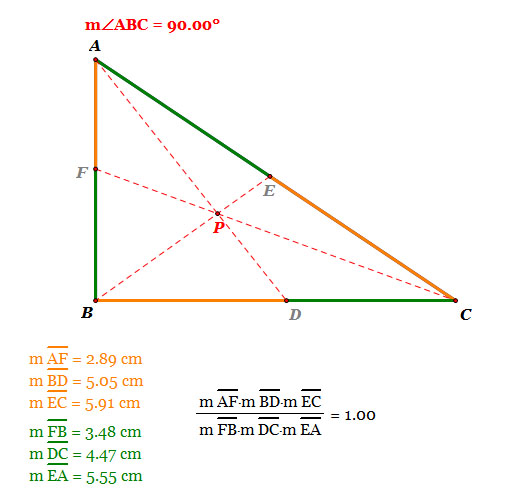
RightTri_ratio

  • As we see, when the triangle ABC is a right triangle, the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) is 1.
3. When triangle ABC is a ACUTE triangle

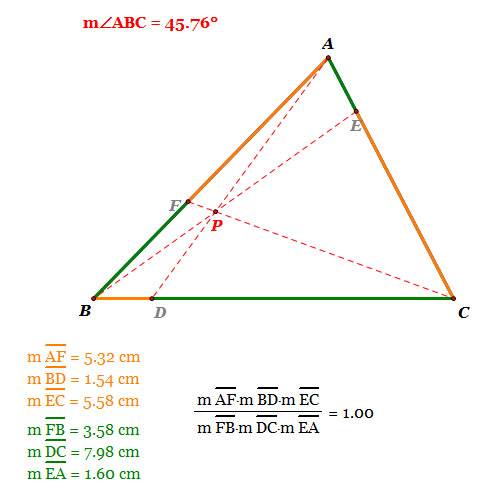
AcuteTri_ratio

  • As we see, when the triangle ABC is an acute triangle, the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) is 1.

* If you want to see these in GSP movie, please click here. >>> Ceva's Theorem when P is inside

Construction 2

: when point D is moving
1. When point D is on the side BC

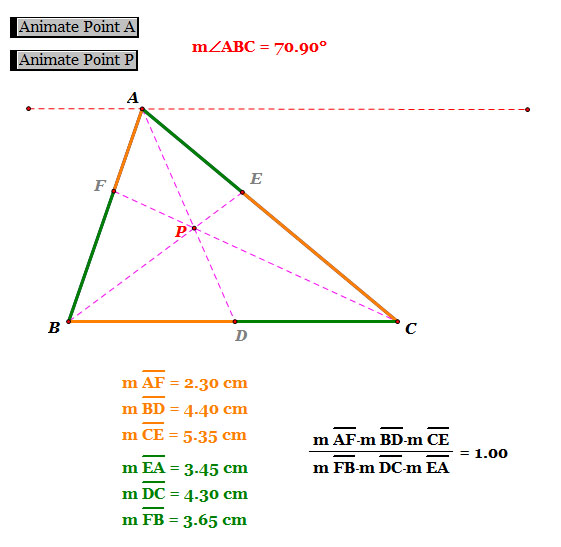
OnSide_ratio

  • As we see, when point D is on the side BC, i.e. point P is inside triangle ABC, the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) is 1.
2. When point D is at the Left end point B

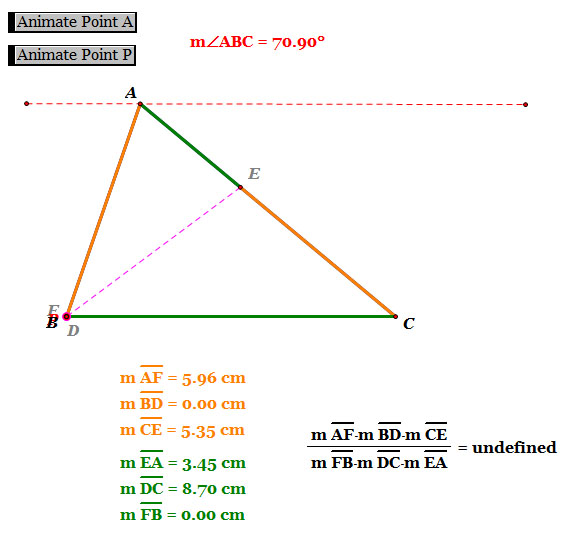
EndpointL_ratio

  • As we see, when point D is at the Left end point B, i.e. point P is at the vertex of the triangle A, the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) is undefined because the length of line segment FB is 0.
3. When point D is at the Right end point B

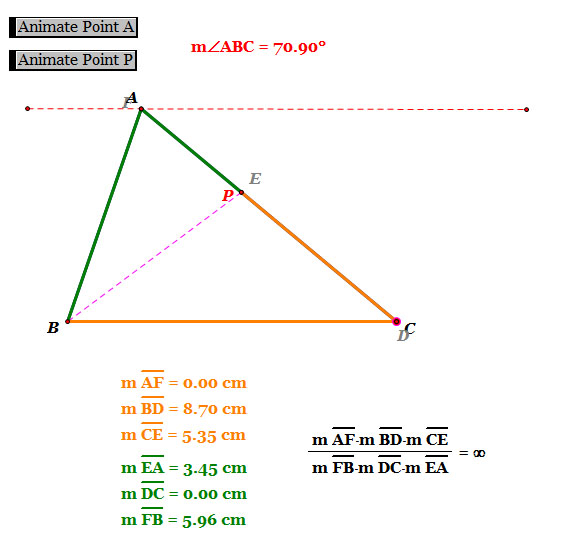
EndpointR_ratio

  • As we see, when point D is at the Left end point B, i.e. point P is on the side of the triangle ABC, the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) is infinity because the length of line segment AF is 0.

* If you want to see these in GSP movie, please click here. >>> Ceva's Theorem when D is moving

Conclusion

 
  • When the point P is inside the triangle ABC, the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) is always 1.
  • When the point D is moving along the line segment BC, the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) is

    '1' if point D is on the side BC, i.e. point P is inside triangle ABC
    'UNDEFINED'     if point D is at the Left end point B, i.e. point P is at the vertex of the triangle
    'INFINITY'     if point D is at the Left end point B, i.e. point P is on the side of triangle ABC

Back to the Top


2. Proof of Ceva's Theorem (when point P is inside of triangle ABC)

Construction

    

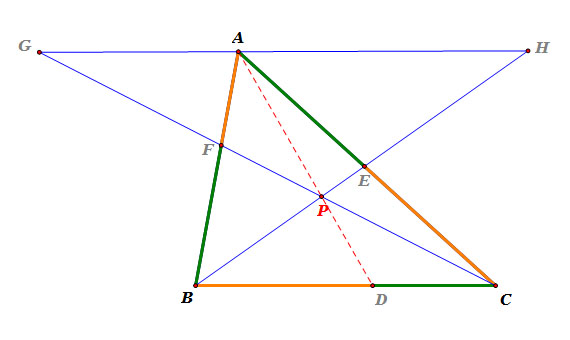
Proof1
  1. Draw a line that parallel to side BC and passes through point A, and name it line k.
  2. Extend line segment CF, and find an intersecting point of line k and ray CF. Name the point as point G.
  3. Extend line segment BE, and find an intersecting point of line k and ray BE. Name the point as point H.

Step 1
: Use triangle EHA and triangle EBC

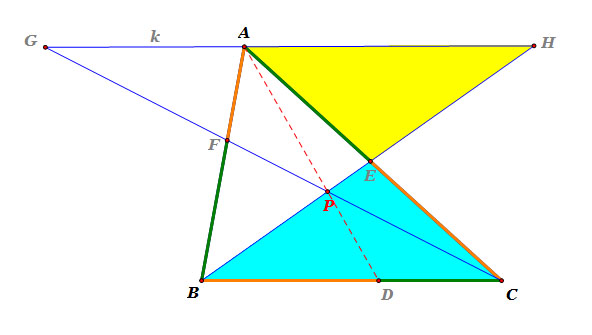
Proof2
 

Consider triangle AEH and triangle CEB.

Since line k and line segment BC are parallel and line segment AC and line segment HB are tranversal,

m( angle AHE) = m(angle CBE) <<< corresponding angles
m( angle HAE) = m(angle BEC) <<< corresponding angles
m( angle AEH) = m(angle CEB) <<< vertical angles.

So, triangle AEH and triangle CEB are similar.

Thus, m(line segment CE) : m(line segment AE) = m(line segment CB) : m(line segment AH),
i.e. m(line segment CE) / m(line segment AE) = m(line segment CB) / m(line segment AH).
Step 2
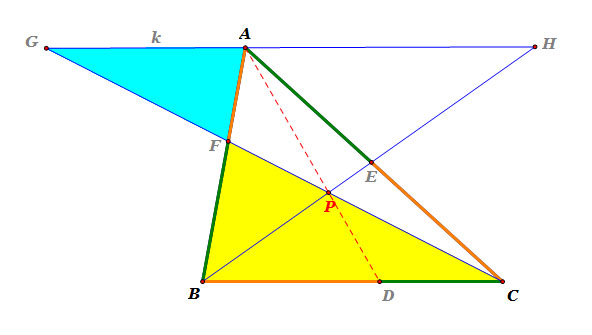
: Use triangle AGF and triangle BCF		   Proof3
 

Consider triangle AGF and triangle BCF.

Since line k and line segment BC are parallel and line segment GC and line segment AB are tranversal,

m( angle AGF) = m(angle BCF) <<< corresponding angles
m( angle GAF) = m(angle CBF) <<< corresponding angles
m( angle AFG) = m(angle BFC) <<< vertical angles.

So, triangle AGF and triangle BCF are similar.

Thus, m(line segment AF) : m(line segment BF) = m(line segment AG) : m(line segment BC),
i.e. m(line segment AF) / m(line segment BF) = m(line segment AG) / m(line segment BC).
Step 3
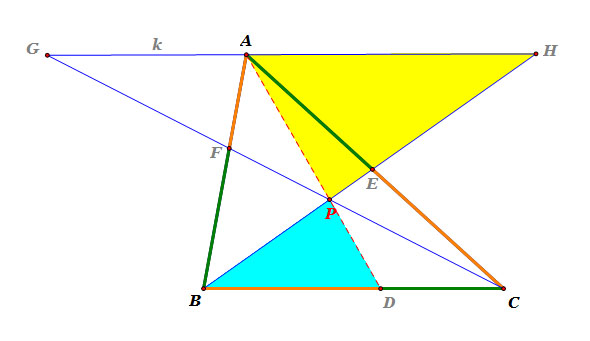: Use triangle APH and triangle DPB		   Proof4
 

Consider triangle APH and triangle DPB.

Since line k and line segment BC are parallel and line segment AD and line segment HB are tranversal,

m( angle AHP) = m(angle DBP) <<< corresponding angles
m( angle HAP) = m(angle BDP) <<< corresponding angles
m( angle APH) = m(angle DPB) <<< vertical angles.

So, triangle APH and triangle DPB are similar.

Thus, m(line segment AP) : m(line segment DP) = m(line segment AH) : m(line segment CB),
i.e. m(line segment AP) / m(line segment DP) = m(line segment AH) / m(line segment DB).

Step4
: Use triangle AGP and triangle DCP

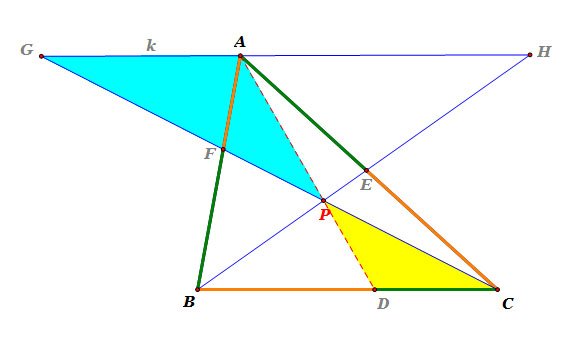   Proof5
 

Consider triangle AGP and triangle DCP.

Since line k and line segment BC are parallel and line segment AD and line segment GC are tranversal,

m( angle AGP) = m(angle DCP) <<< corresponding angles
m( angle GAP) = m(angle CDP) <<< corresponding angles
m( angle APG) = m(angle DPC) <<< vertical angles.

So, triangle AGP and triangle DCP are similar.

Thus, m(line segment AP) : m(line segment DP) = m(line segment AG) : m(line segment BC),
i.e. m(line segment AP) / m(line segment DP) = m(line segment AG) / m(line segment DC).
Step 5
: Use the proportions		    

Since

m(line segment CE) / m(line segment AE) = m(line segment CB) / m(line segment AH)
m(line segment AF) / m(line segment BF) = m(line segment AG) / m(line segment BC)
m(line segment AP) / m(line segment DP) = m(line segment AH) / m(line segment DB)
m(line segment AP) / m(line segment DP) = m(line segment AG) / m(line segment DC),

[ m(line segment AF) * m(line segment BD) * m(line segment EC) ] / [ m(line segment FB) * m(line segment DC) * m(line segment EA) ]
= [ m(line segment AF) / m(line segment FB) ] * [ m(line segment EC) / m(line segment EA) ] * [ m(line segment BD) / m(line segment DC) ]
= [ m(line segment AG) / m(line segment BC) ] * [ m(line segment CB) / m(line segment AH) ] * [ m(line segment BD) / m(line segment DC) ]
= [ m(line segment AG) / m(line segment AH) ] * [ m(line segment BD) / m(line segment DC) ]
= [ m(line segment AG) /m(line segment DC) ] * [ m(line segment BD) / m(line segment AH) ]
= [ m(line segment AP) / m(line segment DP) ] * [ m(line segment DP) / m(line segment AP) ]
= 1

Back to the Top


3. Proof of three Medians' Concurrency

 

Construction

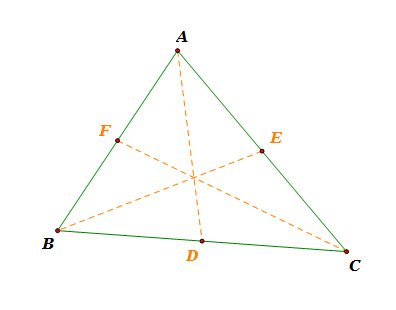
     Median1

Proof

There are three medians, line segment AD, line segment BE, and line segment CF.

Since m(line segment AF) = m(line segment BF), m(line segment BD) = m(line segment CD), and m(line segment CE) = m(line segment AE),
[ m(line segment AF) * m(line segment BD) * m(line segment CE) ] / [ m(line segment BF) * m(line segment CD) * m(line segment AE) ] = 1.

So, the three medians should intersect at one point, and that point is point P in Ceva's Theorem.

Hence, we can prove the concurrency of three medians from Ceva's Theorem.
 

Back to the Top


4. Proof of Ceva's Theorem (when point P is outside triangle ABC)

 

Construction
for Ceva's Theorem

 

    

When the intersection of three Cevians, point P, is outside triangle ABC, the construction for Ceva's Theorem looks like this:

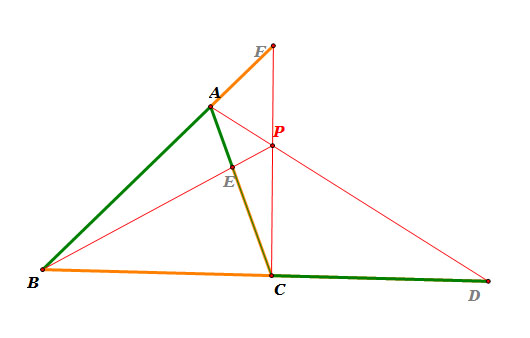
POut1
Construction for Proof
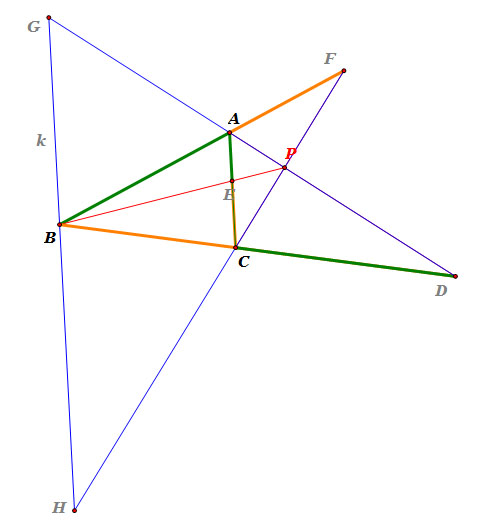 POut2
  1. Draw a line that parallel to side AC and passes through point B, and name it line k.
  2. Extend line segment DA, and find an intersecting point of line k and ray DA. Name the point as point G.
  3. Extend line segment FC, and find an intersecting point of line k and ray FC. Name the point as point H.

Step 1
: Use triangle DGB and triangle DAC

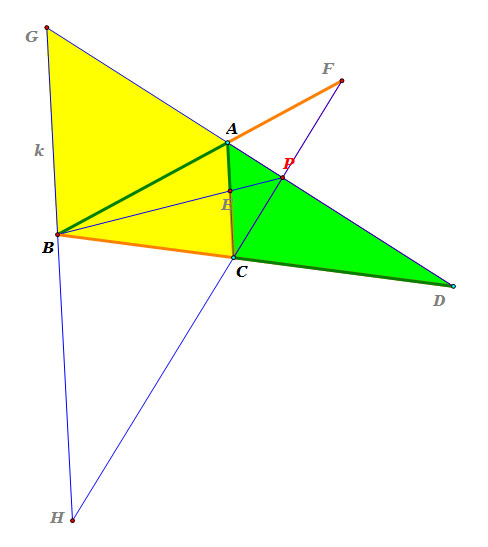
POut3

Consider triangle DGB and triangle DAC.

Since line k and line segment AC are parallel and line segment DG and line segment DB are tranversal,

m( angle DAC) = m(angle DGB) <<< corresponding angles
m( angle DCA) = m(angle DBG) <<< corresponding angles
m( angle ADC) = m(angle GDB) <<< common angles.

So, triangle DGB and triangle DAC are similar.

Thus, m(line segment BD) : m(line segment DC) = m(line segment GB) : m(line segment AC),
i.e. m(line segment BD) / m(line segment DC) = m(line segment GB) / m(line segment AC).
Step 2
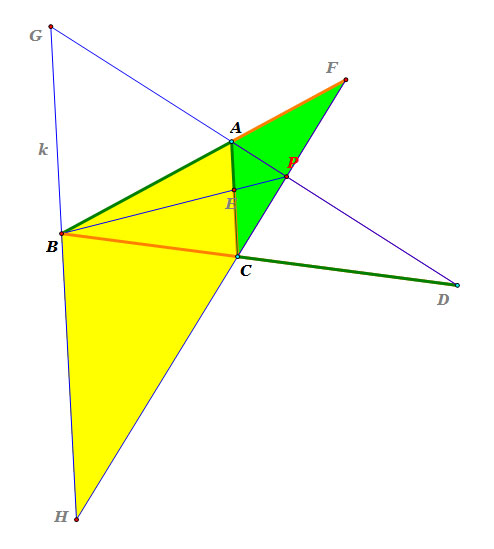: Use triangle FBH and triangle FAC		 POut4

Consider triangle FBH and triangle FAC.

Since line k and line segment AC are parallel and line segment FB and line segment FH are tranversal,

m( angle FAC) = m(angle FBH) <<< corresponding angles
m( angle FCA) = m(angle FHB) <<< corresponding angles
m( angle AFC) = m(angle BFH) <<< common angles.

So, triangle FBH and triangle FAC are similar.

Thus, m(line segment AF) : m(line segment FB) = m(line segment AC) : m(line segment BH),
i.e. m(line segment AF) / m(line segment FB) = m(line segment AC) / m(line segment BH).

Step 3
: Use triangle PBH and triangle PEC

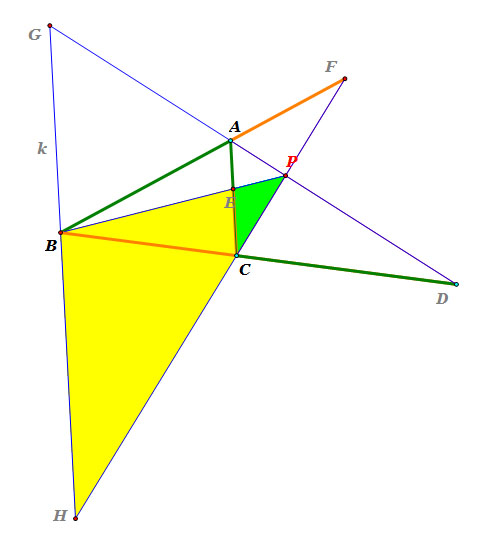 POut5

Consider triangle PBH and triangle PEC.

Since line k and line segment EC are parallel and line segment PB and line segment PH are tranversal,

m( angle PEC) = m(angle PBH) <<< corresponding angles
m( angle PCE) = m(angle PHB) <<< corresponding angles
m( angle EPC) = m(angle BPH) <<< common angles.

So, triangle PBH and triangle PEC are similar.

Thus, m(line segment EC) : m(line segment BH) = m(line segment PE) : m(line segment PB),
i.e. m(line segment EC) / m(line segment BH) = m(line segment PE) / m(line segment PB).
Step 4
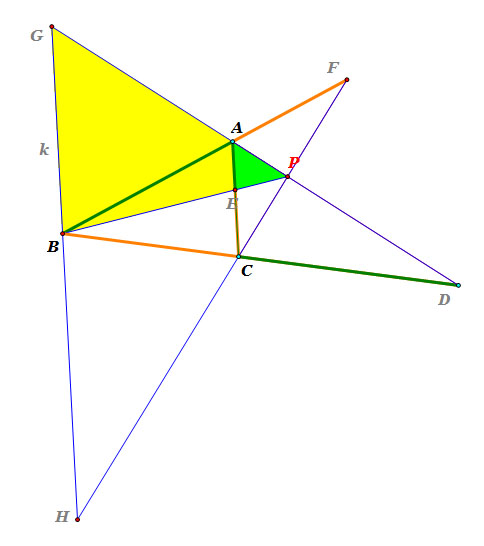: Use triangle PGB and triangle PAE		 POut6

Consider triangle PGB and triangle PAE.

Since line k and line segment EC are parallel and line segment PG and line segment PB are tranversal,

m( angle PAE) = m(angle PGB) <<< corresponding angles
m( angle PEA) = m(angle PBG) <<< corresponding angles
m( angle APE) = m(angle GPB) <<< common angles.

So, triangle PGB and triangle PAE are similar.

Thus, m(line segment GB) : m(line segment AE) = m(line segment PB) : m(line segment PE),
i.e. m(line segment GB) / m(line segment AE) = m(line segment PB) / m(line segment PE).

Step 5
: Use the proportions

Since

m(line segment BD) / m(line segment DC) = m(line segment GB) / m(line segment AC)
m(line segment AF) / m(line segment FB) = m(line segment AC) / m(line segment BH)
m(line segment EC) / m(line segment BH) = m(line segment PE) / m(line segment PB)
m(line segment GB) / m(line segment AE) = m(line segment PB) / m(line segment PE),

[ m(line segment AF) * m(line segment BD) * m(line segment EC) ] / [ m(line segment FB) * m(line segment DC) * m(line segment EA) ]
= [ m(line segment AF) / m(line segment FB) ] * [ m(line segment BD) / m(line segment DC) ] * [ m(line segment EC) / m(line segment EA) ]
= [ m(line segment AC) / m(line segment BH) ] * [ m(line segment GB) / m(line segment AC) ] * [ m(line segment EC) / m(line segment EA) ]
= [ m(line segment GB) /m(line segment BH) ] * [ m(line segment EC) / m(line segment EA) ]
= [ m(line segment GB) /m(line segment EA) ] * [ m(line segment EC) / m(line segment BH)]
= [ m(line segment PB) / m(line segment PE) ] * [ m(line segment PE) / m(line segment PB) ]
= 1

Button Go Back to Top
Button Go Back to Michelle's Main page
Button Go Back to EMAT 6680 Homepage
Copyright @ Michelle E. Chung