Gayle Gilbert & Greg Schmidt

In this problem we are given the following table of incomplete information:

Age of Tree	100s board feet
20	1
40	6
60
80	33
100	56
120	88
140
160	182
180
200	320

We would like to use Excel To complete the given table of information.

We begin by using the given information to create a scatter plot graph, which gives us:

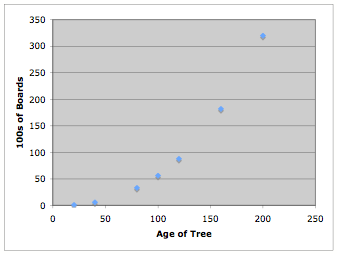
The scatter plot appears to closely fit some power or exponential function. We can click on the given graph when in Excel, and add a trend line to the data points. The following graph is the trend line for a power function:

Our first choice appears to fit the data points rather well, but we will also examine the trend lines given when the exponential and polynomial fit is selected. Notice that Excel has also given us the power function for the scatter points, which is . We also note that the R squared value is given at , which indicates the power function strongly fits our data points.

For the polynomial trend line we have:

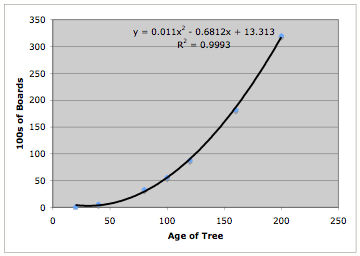
This also appears to be a good fit, but we notice that Excel provides and R squared value of , and so the polynomial function does not fit our data points as well as the power function.

Finally, we consider the exponential function fit to our data points.

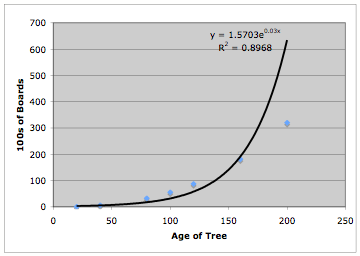
We immediately see that this choice is not as good of a fit as the power function fit to our data points.

Hence, we will use the power function fit to our data points of to complete our incomplete table.

So we have:

Age of Tree	100s board feet
20	1
40	6
60	16
80	33
100	56
120	88
140	134
160	182
180	251
200	320

How would this differ if instead we used the polynomial function fit to our data points?

Notice using the given polynomial function to complete our table we have:

Age of Tree	100s board feet
20	1
40	6
60	12
80	33
100	56
120	88
140	134
160	182
180	247
200	320

So our tables differ only for tree age 60 and 180…so isn’t that just dandy!

Return