A Question of Equivalence

Many students have ill-defined notions of 'equivalence.' They may loosely regard it as equal, or similar. Since an enumeration of formal rules of logic may be too large a dose of medicine for their particular ailment, share with them an example where two ideas are not equivalent. One classic example is the following:

Let A be the idea: I see a healthy, normal cow.

Let B be the idea: I see an animal with 4 legs.

A implies B, that is, "If I see a healthy, normal cow then I see an animal with 4 legs" is true.

B does not imply A, that is, "If I see an animal with 4 legs then I see a healthy, normal cow" is not necessarily true.

The idea of equivalence is that each idea requires the other. So, if we have ideas C and D, both statements "If C then D" and "If D then C" must be true. In our case, we desire to check the equivalence of 3 ideas - let's list them as follows:

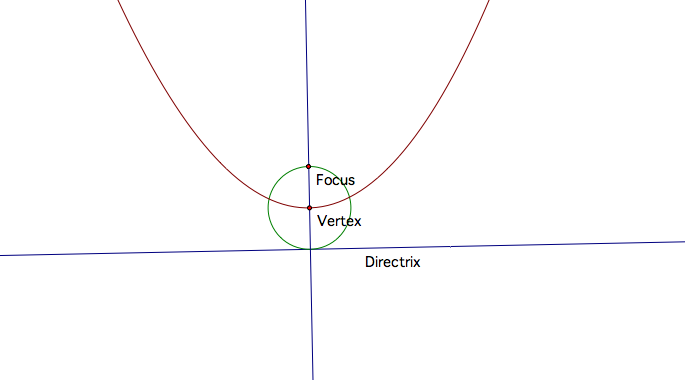
A: Given a parabola, one may construct the vertex.

B: Given a parabola, one may construct the focus.

C: Given a parabola, one may construct the directrix.

We have a bit of flexibility in proving the equivalence of three ideas. Ask the students to arrange a possible chain of implications that would prove equivalence. For example, they might write:

A implies B. B implies C. C implies A. as one such chain

A implies B. B implies A. A implies C. C implies A. B implies C. C implies B. is another such chain.

One additional spot of likely trouble for them involves the assumption of the hypothesis to prove the conclusion. For example, if they are asked to prove "If I can construct the directrix, then I can construct the vertex." they may resist by saying, "But what if I can't construct the directrix?" or they may be unwilling to actually utilize the directrix in their proofs. This type of claim represents a fundamental question of logic, and should not be ignored if it arises.

Once you are somewhat confident that your students are okay with the idea of equivalence, they should try and prove one of the implications in their chain. While there are many possible chains and also many possible methods of proof, a few are briefly illustrated here:

C implies B

 

B implies A

This consideration is rather trivial if one considers our proof of finding the vertex from just the parabola's graph, much less the graph and the vertex.

 

B implies C

Here again we can use the fact that we can construct the vertex without anything else.