Tiffany N. KeysŐ Assignment 9:
Pedal
Triangles
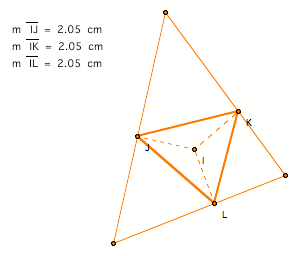
Let triangle ABC be any triangle. Then if P
is any point in the plane, then the triangle formed by constructing
perpendiculars to the sides of ABC (extended if necessary) locate three points
R, S, and T that are the intersections. Triangle RST is the Pedal
Triangle for
Pedal Point P.
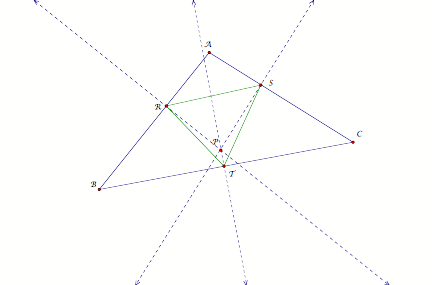
What if Pedal Point is coincident with the
centroid of triangle ABC?
The
centroid of a triangle is the common intersection of the three medians. A
median of a triangle is the segment from a vertex to the midpoint of the
opposite side.
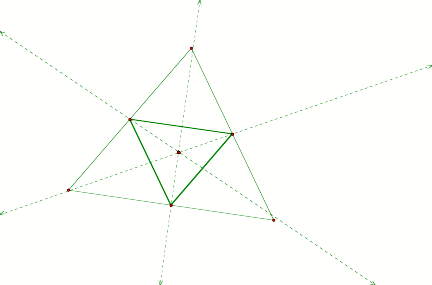
When
the pedal point is coincident with the centroid of a triangle, the pedal
triangle will be similar to the larger triangle, therefore dividing it into
four similar triangles.
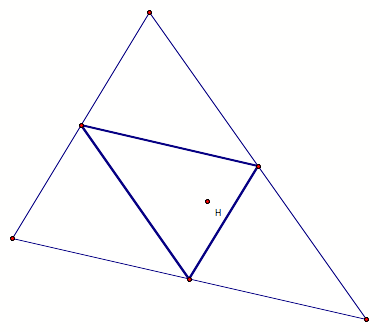
What if the Pedal Point is coincident with
the orthocenter of triangle ABC?
The
orthocenter of a triangle is the common intersection of the three lines
containing the altitudes. An altitude is a perpendicular segment from a vertex
to the line of the opposite side.
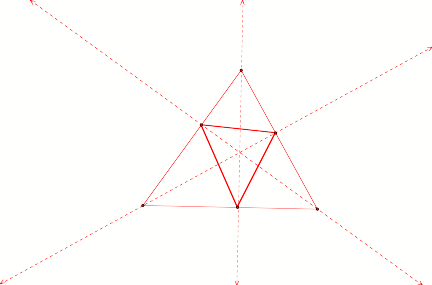
What if the Pedal Point is coincident with
the circumcenter of triangle ABC?
The
circumcenter of a triangle is the point in the plane equidistant from the three
vertices of the triangle. Since a point equidistant from two points lies on the
perpendicular bisector of the segment determined by two points, the
circumcenter is on the perpendicular bisector of each side of the triangle.
What if the Pedal Point is coincident with
the incenter of triangle ABC?
The
incenter of a triangle is the point on the interior of the triangle that is
equidistant from the three sides.