Tiffany N. KeysŐ Assignment 2:

Look at that Parabola!

 

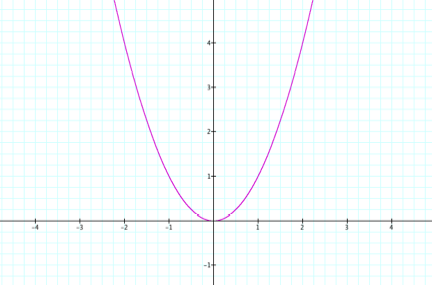
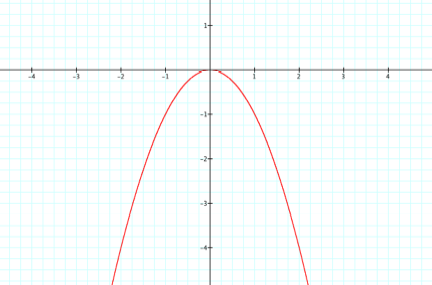
A quadratic function has the form y = ax2 + bx +c, where a is not equal to zero. The U-shaped graph of a quadratic function is called a parabola. The graphs of all quadratic functions are related to the graphs y = x2 and y = - x2

 

y = x2                                                                                                                                                                  y = - x2

                                     

 

These graphs have the following characteristics:

¤     The origin is the lowest point on the graph of y = x2 and the highest point of the graph of y = -x2

¤     The lowest point or the highest point on the graph of a quadratic function is called the vertex.

¤     The axis of symmetry for the graph of a quadratic function is the vertical line through the vertex. The graphs above are both symmetric about the axis of symmetry or, in these cases, the y – axis. 

 

 

INVESTIGATION: Construct graphs for the parabola y = ax2 + bx +c for different values of a, b, and c.

 

 

First, letŐs begin with substituting in values for a:

 

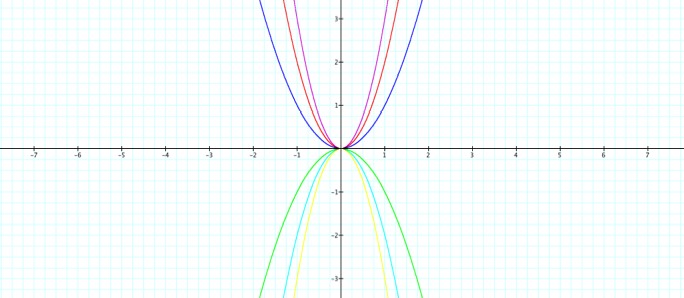
                                          Y = 3x2                               y = 2x2                        y = x2

Y = -3x2                              y = -2x2                       y = -x2

 

OBSERVATIONS:

á      The parabola always passes through the origin.

á      The coordinates of the vertex of the parabola do not change in each equation as different values for a are substituted in.

á     The concavity of the parabola is the aspect of the graph changes in each equation. As a increases, the concavity of the parabola decreases. If a is negative, then it is reflected across the x-axis.

 

Next, letŐs observe what happens when different values for b are substituted in:

 

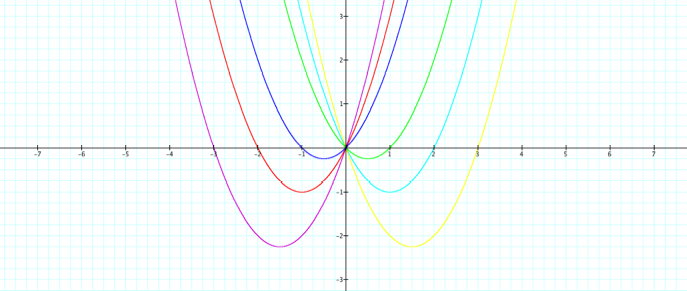
                                    Y = x2+3x                      y = x2+2x                    y = x2 + x

Y = x2- 3x                      y = x2- 2x                   y = x2 - x

 

OBSERVATIONS:

á      As above, the parabola always passes through the origin.

á     However, the coordinates of the vertex of the parabola are the aspect of the graph that changes in each equation. As b increases, the vertex shifts across the x-axis. If b is negative, then it reflected across the y-axis.

á     The concavity of each parabola does not change in each equation as different values of b are substituted in.

 

Lastly, letŐs notice the difference in the graph when values for c are substituted in:

 

                                    Y = x2+ x + 3                 y = x2 + x + 2                  y = x2 + x + 1

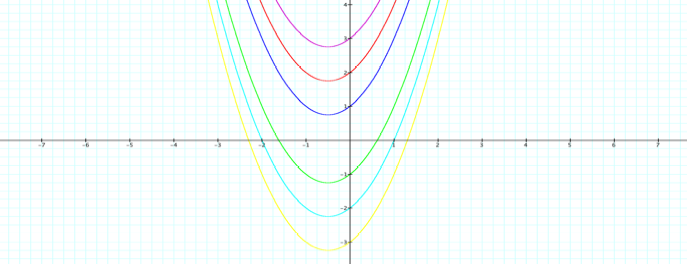
                                    Y = x2+ x - 3                 y = x2 + x - 2                   y = x2 + x - 1

 

OBSERVATIONS:

á      The parabola does not pass through the same point as c changes.

 

 

Return to Tiffany N. KeysŐ Homepage