
Tiffany N. KeysŐ Assignment 4:
Concurrency
and Perpendicular Bisectors
INVESTIGATION: Prove that the three perpendicular
bisectors of the sides of a triangle are concurrent.
Step 1:
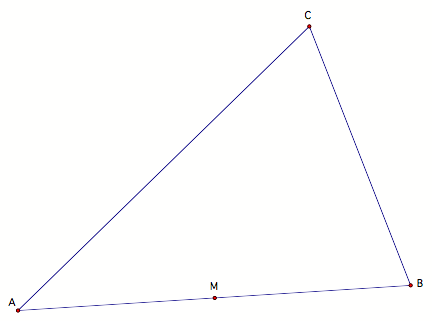
Given triangle ABC,
construct the midpoint, M, of AB.
Step 2:
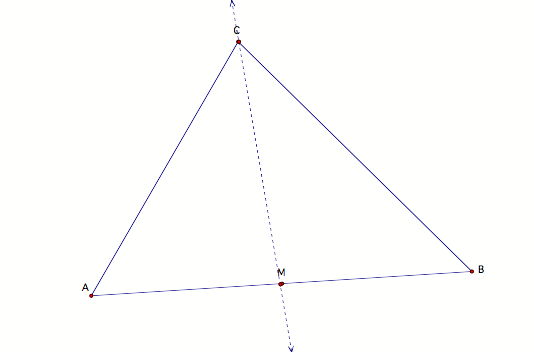
Construct the
perpendicular bisector, x, of AB.
Step 3:

Construct a point, D,
on x, then construct DA and DB
Step 4:
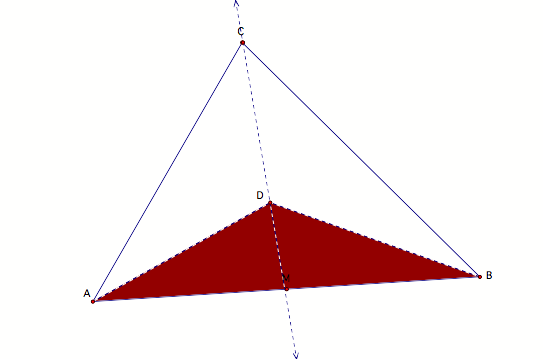
Since AM = BM,
angle(AMD) = angle(BMD).
Since triangle(AMD) =
triangle(BMD) by the Side-Angle-Side Theorem. Therefore, AD = DB.
Step 5:
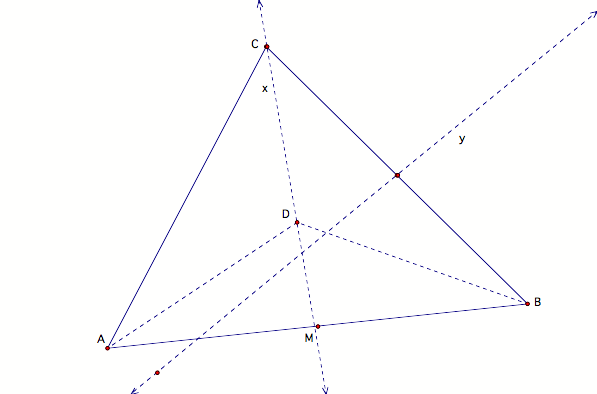
Construct the
perpendicular bisector, y, of BC.
Since AB and BC are
not parallel, lines x and y must intersect.
Step 6:
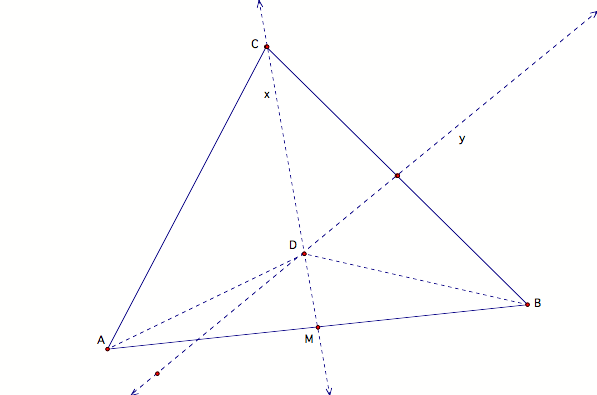
Merge point D to the
point of intersection for lines x and y.
Therefore, CF = FB,
angle (CFD) = angle(BFD), triangle (CFD) = triangle (BFD), and CD = DB.
By the Axiom that
states that every segment is congruent to itself, we know that if CD=DB and
DB=DA, then DA=DC.
Step 7:
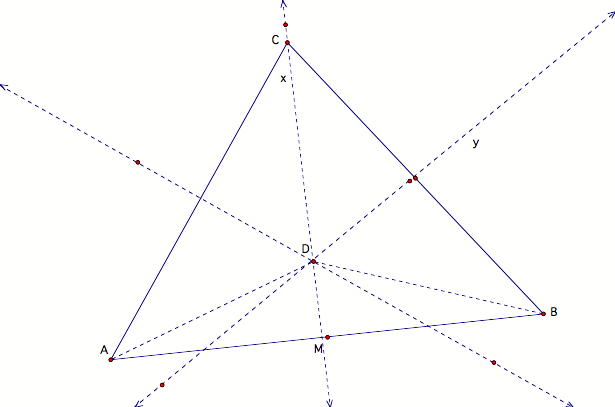
Therefore, D is on
the perpendicular bisector of AC, yielding that the perpendicular bisectors of
the sides of a triangle are concurrent.