Tiffany N. Keys’ Final Assignment:

Ceva’s Thereom

Ceva's Theorem. Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

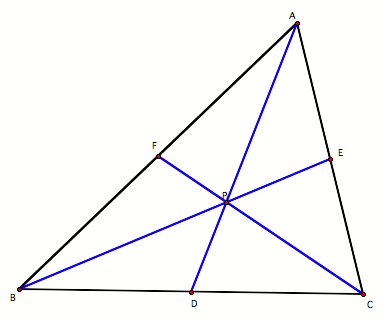
1. Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.



2. Conjecture? Prove it! (you may need draw some parallel lines to produce some similar triangles, OR, you made need to consider areas of triangles within the figure) Also, it probably helps to consider the ratio


(AF)(BD)(CE)

(BF)(CD)(AE)

3. In your write-up, after the proof, you might want to discuss how this theorem could be used for proving concurrency of the medians (if P is the centroid), the lines of the altitudes (if P is the orthocenter), the bisectors of the angles (if P is the incenter), or the perpendicular bisectors of the sides (if P is the circumcenter). Concurrency of other special points?

4. Explore a generalization of the result (using lines rather than segments to construct ABC) so that point P can be outside the triangle. Show a working GSP sketch.


Let’s explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

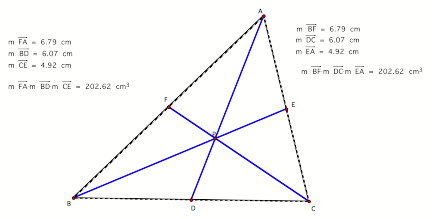
OBSERVATIONS:

· The ratios of (AF)(BD)(EC) and (FB)(DC)(EA) from this triangle with P as the centroid turned out to be equal .

· From looking at this triangle, it was assumed that no matter where P is located, the ratios will always be the same and remain equal.

Ceva's Theorem states:

If the points F, E, and D are on the sides AB, AC and BC of a triangle then the lines AC, BE and CF are concurrent if and only if the product of the ratios

(AF)(BD)(CE)

(FB)(DC)(EA)

PROOF:

1. AF = DACP

FB DBCP

2. BF = DABP

FA DACP

3. CE = DBCP

EA DABP

Therefore, (AF)(BF)(CE) = (DACP)( DABP)( DBCP)

(FB)(FA)(EA) (DBCP)( DACP)( DABP)

Return to Tiffany N. Keys’ Homepage