Carisa Lindsay

Assignment 9:

Pedal Triangles

We can construct the pedal triangle with the perpendicular lines to ABC and their intersections.

If the pedal point P is outside ABC, then the pedal triangle is outside ABC.

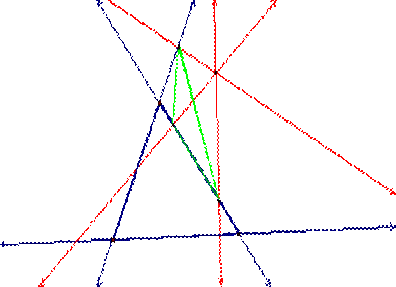
If the pedal point P is inside ABC, then the pedal triangle is also inside ABC.

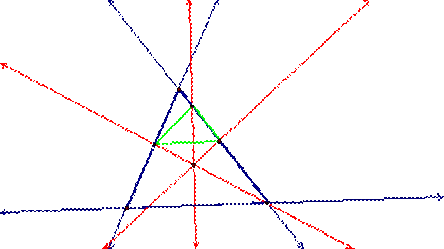
However, if pedal point P is closer to the boundary formed by ABC, then the pedal triangle overlaps this boundary (meaning some of the triangle is inside ABC while some is outside).

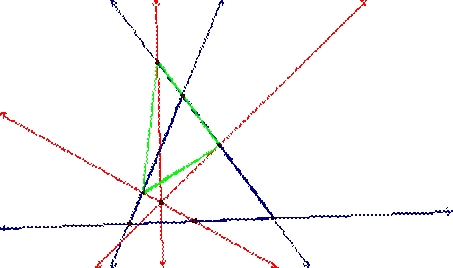
Clearly, we cannot conclude where the pedal triangle will exist solely on the location of pedal point P being inside or outside ABC. So, let’s consider more specific locations of pedal point P.

Let’s explore what happens when point P lies on the various centers of ABC.

Suppose pedal point P is located at the centroid of ABC:

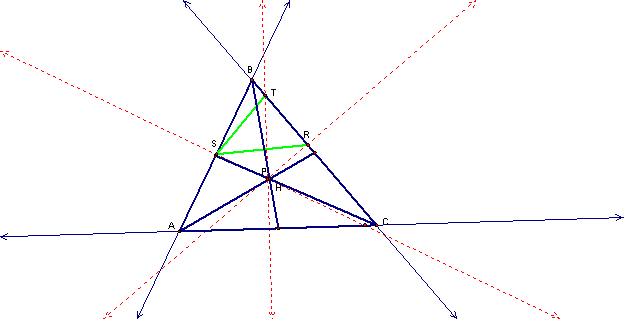
We can see that if point P is at the centroid of ABC, then the pedal triangle is located within the boundaries of ABC.

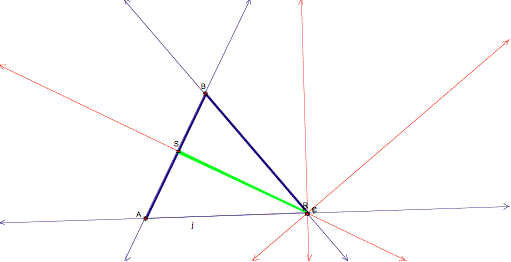
Suppose point P is at the incenter of ABC:

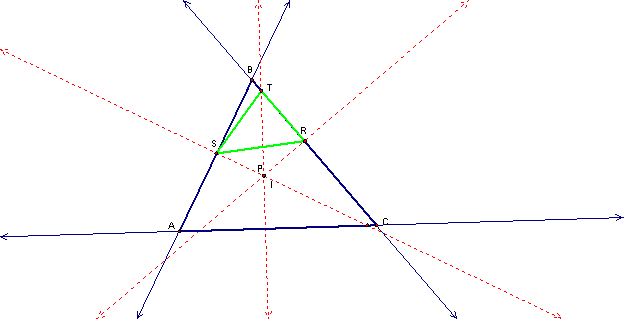
We see similar results as point P being at the centroid. The pedal triangle RST is again within the boundaries of ABC.

Now, let’s consider point P lying on the orthocenter of ABC:

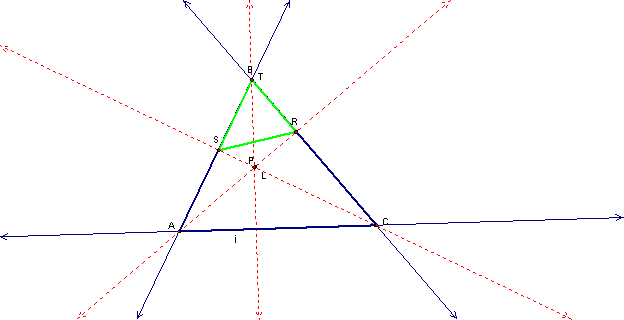
This is particularly interesting because the sides ST and TR align with AB and BC. Again, we see the pedal triangle resides within ABC.

Lastly, let’s consider the circumcenter of ABC:

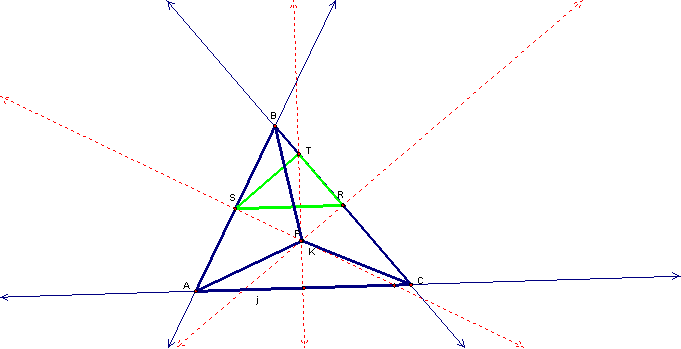
Again, the pedal triangle lies within ABC.

We can conclude the pedal triangle does not exist outside of ABC when pedal point P lies on one of the centers of the ABC.

What happens when we put point P on one of the sides of ABC?

This depends largely on which side of the triangle point P resides and how close point P is to a vertex.

As we move from Vertex A to Vertex B,

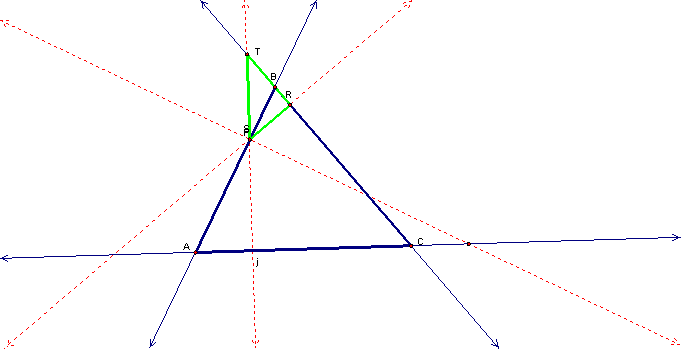
We see the point P lies on one of the vertices of RST, namely S.

However, as point P moves between vertex B and vertex C,

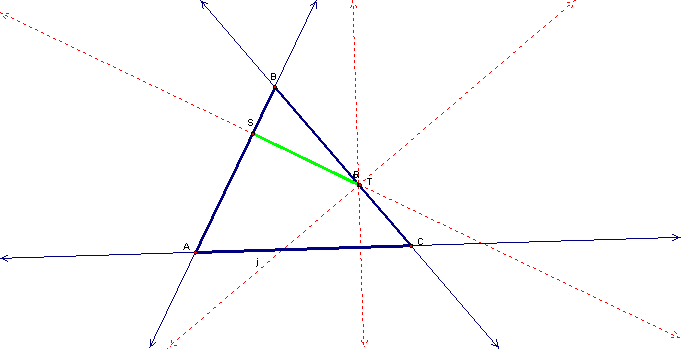
We see that point P lies on both vertex R and vertex T. We do not see the pedal triangle in this case, but rather we see a line segment formed.

Perhaps we should consider what would happen if the pedal point P lies on one of the vertices?

Vertex A:

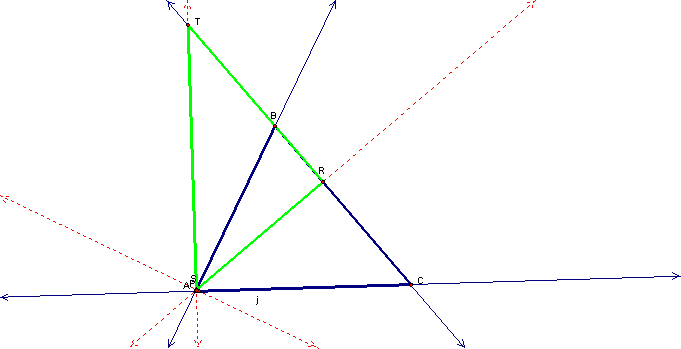
Point P overlaps vertex S in RST.

Vertex B:

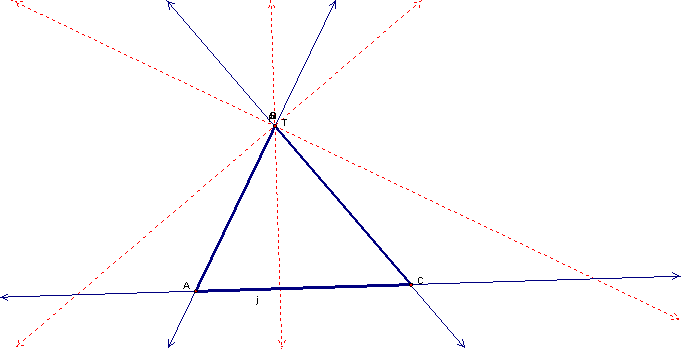
Point P overlaps vertices R, S and T. We do not see a pedal triangle formed.

Vertex C:

We see a line segment created and point P overlaps vertex R and T.

The existence and placement of the pedal triangle depends on which vertex it lies upon. In one case (vertex A), the pedal triangle is a right triangle which extends beyond ABC. In another case (vertex B), the pedal triangle is not formed at all. In the last case (vertex C), the pedal triangle forms into a segment along the perpendicular bisector of side AB.

Return to Lindsay’s Homepage