Carisa Lindsay

Final Project

Bouncing Barney

For any triangle ABC, the problem arises when trying to figure out how many times Barney will touch the sides of the triangle as he travels parallel to each side.

Using Geometer’s Sketchpad, we can construct an arbitrary triangle with Barney beginning at some arbitrary point D. We can see through constructing parallel lines and intersections that Barney will hit the wall six times.

However, this is not the case when Barney begins at any vertex,

or when Barney begins at the midpoint of any side.

Click here to see animation

What if Barney begins at the centroid?

If Barney begins at the centroid of triangle ABC, he will reach the wall only reaches twice before returns back to his starting place. However, he will not actually STOP at his at his starting place, but will instead pass through the starting place. As he passes through his original starting place, he will maintain a similar path as before.

What is the fewest number of times Barney can reach the wall and still return to his original starting place? Let’s consider triangle ABC as a right triangle.

What if Barney begins at one of the vertices? If Barney begins at a vertex, he will not move since he will be unable to move parallel to the opposite side due to the boundary of the room.

Suppose Barney begins his journey outside of ABC.

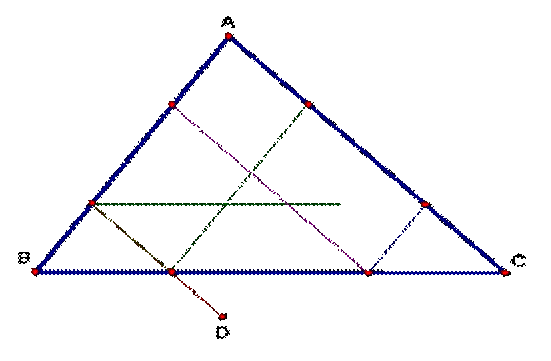
Regardless of where Barney begins, we see a similar pattern with how he “bounces” around the triangle. Again, he will hit the wall six times before returning to a location he has already been to. However, Barney will never reach the point in which he began because of being constrained within the boundaries of the triangle. Much of this problem depends on the “rules” for which directions Barney is allowed to travel.

This would be an appropriate activity in a secondary geometry class studying parallel lines and their transversals, as well as interior angles resulting from them. Furthermore, a physics class could use a problem like this when studying angles of deflection of light.

So how far is Barney bouncing?

The answer is not obvious. First, we need to divide Barney’s paths into various line segments so we can create parallelograms. Because these sections are parallelograms and using the definition of parallelograms, we can see that various sides are congruent.

Since these sides are congruent, they remain congruent as Barney travels. As barney approaches a vertex, it is more obvious that Barney is actually traveling the same distance as the perimeter of the “room”.

Click here for animation.

Return to Lindsay’s Homepage