Problem Statement:

Graph x² + y² = 1, x³ + y³ = 1, x⁴ + y⁴ = 1, and x⁵ + y⁵ = 1. What do you expect for x²⁴ + y²⁴ = 1 and x²⁵ + y²⁵ = 1?

by Laura Lowe

I began by graphing the 4 relations as shown below. 

I can immediately see that there is a relationship between graphs of the red and blue functions and those of the purple and green functions.  When I look at the equations of those graphs, it becomes clear that there is likely some kind of relationship involving odd and even exponents. It appears upon my initial examination that the relations with even exponents have a circular shape. In fact the first relation, x² + y² = 1 is a circle with radius 1 centered at the origin, as we should have expected from the equation. However, the next even powered relation, x⁴ + y⁴ = 1 also has a circular shape, but with the corners extended out to look more like a square. This relation also has a radius of 1 along the x-axis and the y-axis, but nowhere else. I can also see that the relations with the odd exponents look like the line y = -x with a ”bump” out into Quadrant I. That “bump” has a circular appearance in x³ + y³ = 1, but appears more square.

From this I can establish an initial hypothesis that the equations of the form xⁿ + yⁿ = 1 will, when n is even, have a circular appearance that becomes more like a square as the exponents become larger, and, when n is odd, look like the line y = -x, but with a “bump” into Quadrant I that also becomes more square in shape as the exponents become larger.

In order to further investigate this relationship, I graphed the function xⁿ + yⁿ = 1 where n = 2, 4, 6, 8, and 10.

From these graphs I can see my hypothesis holds true. The graphs of xⁿ + yⁿ = 1, when n is even, look like a circle with the corners gradually being dragged outward into a square shape as we increase n. Click here to see an animation.

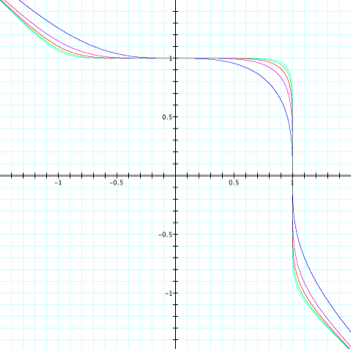
Similarly, I graphed the function xⁿ + yⁿ = 1 where n = 3, 5, 7, 9, and 11.

Again I can see my hypothesis holds true. The graphs of xⁿ + yⁿ = 1, when n is odd, look like the line y = -x with a “bump” into Quadrant I that becomes more square in shape as we increase n. Click here to see an animation.

So I expect that x²⁴ + y²⁴ = 1 and x²⁵ + y²⁵ = 1 will have the same characteristics. When I graph them,

I can see that my hypothesis was correct. I will leave it up to you to decide which graph is which.

Extensions:

Why doesn’t xⁿ + yⁿ = 1 have any points in Quadrant III when n is odd?

What if we were to graph y = xⁿ? Could we expect to see a similar pattern?

What about x = yⁿ?

What should we expect to see if we let n grow infinitely large?

Return