Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

Using GSP, I created a sketch to explore (AF)(BD)(EC) and (FB)(DC)(EA). This exploration leads me to believe that the two products are equal regardless of where P is located within the triangle ABC. Saying that these products are equal is equivalent to saying that their ratio is 1. In other words, ( (AF)(BD)(EC)) / ((FB)(DC)(EA)) = 1.

I constructed lines through P and parallel to each of the sides of the triangle ABC. This creates multiple similar triangles.

-------

(1)

triangle AFC is similar to triangle IPC.

triangle BCF is similar to triangle CPL

This gives us the following equivalent ratios:

AF/IP = CF/CP and FB/PL = CF/CP

So, AF/IP = FB/PL and we can multiply both sides by IP/FB to get AF/FB = IP/PL.

-------

(2)

triangle ABD is similar to triangle GAP

triangle ADC is similar to triangle APJ

This gives us the following ratios:

BD/GP = DA/PA and DC/PJ = DA/PA

So, BD/GP = DC/PJ and we can multiply both sides by GP/DC to get BD/DC = GP/PJ.

--------

(3)

triangle EBC is similar to triangle BPK

triangle AEB is similar to triangle HPB

This gives us the following ratios:

EC/PK = BE/BP and AE/HP = BE/BP

So, EC/PK = AE/HP and we can multiply both sides by PK/AE to get EC/AE = PK/HP

------

(4)

triangle ABE is similar to IPE (because IP is parallel to AB)

So, IP/AB = PE/BE

------

(5)

triangle ABD is similar to triangle LDP

So, LP/AB = PD/AD

-----

(6)

Dividing 4 and 5, we can now get that (IP/AB)/(LP/AB) = (PE/BE)/(PD/AD)

which simplifies to

IP/LP = (PE/BE)/(PD/AD)

------

(7) Substituting (1) into 6, we get

AF/FB = IP/PL = (PE/BE)/(PD/AD)

AF/FB = (PE/BE)/(PD/AD) = ((PE)(AD))/((BE)(PD))

------

(8) triangle FBC is similar to triangle FGP ( because GP is parallel to BC)

So, GP/BC = PF/FC

------

(9) triangle BEC is similar to triangle PEJ (because PJ is parallel to BC).

So, PJ/BC = PE/BE

----

(10) Dividing (8) and (9), we get

(GP/BC)/(PJ/BC) = (PF/FC)/(PE/BE)

GP/PJ = ((PF)(BE))/((FC)(PE))

-----

(11)

Substituting (2) into (10) we get

BD/DC = ((PF)(BE)/(PE)(CF))

------

(12) triangle ADC is similar to triangle PDK (because PK is parallel to EC).

So PK/ AC= PD/AD

-------

(13) triangle AFC is similar to FHP (because HP is parallel to AC)

HP/ AC= PF/CF

-----

(14)

Dividing (12) and (13) we get

PK/HP = (PD/AD)/(PF/CF) = ((PD)(CF)/(PF)(AD))

------

(15)

Substituting (3) into (14) we get

CE/EA = ((PD)(CF)/(PF)(AD))

------

Multiplying (7), (11), and (15) we get

(AF/FB)(BD/DC)(CE/EA) = ((PE)(AD) (PF)(BE)(PD) (CF)) /( (BE)(PD)(PE) (CF) (PF)(AD)) = 1

So finally, we have (AF)(BD)(CE) = (FB)(DC)(EA)

Ceva's Theorem states in a triangle ABC, three lines AD, BE and CF intersect at a single point P if and only if
((AF)(BD)(CE))/((FB)(DC)(EA))= 1.

Proof: Argument above shows that if AD, BE, and CF intersect at a point P then the given ratio is 1.

Now, we will prove it in the other direction. Start with a triangle ABC, with points DEF such that (AF)(BD)(CE)/(FB)(DC)(EA) = 1.

Let P be the intersection of BE and FC. Draw a line From A through P until it intersects BC at point H.

Now we know, from what we just proved that

(AF)(BH)(CE)/(FB)(HC)(EA) = 1

So, (AF)(BD)(CE)/(FB)(DC)(EA) = (AF)(BH)(CE)/(FB)(HC)(EA)

Simplifying we get BD/DC = BH/HC

Now to compare the two ratios let's make both numerators the full length of BC.

BD/DC + DC/DC = BH/HC + HC/HC

This is equivalent to adding one to both sides, so we still have equality.

BC/DC = BC/HC

This can only be true if D and H are the same point.

Special Case of P:

What if D,E, and F are the midpoints of the sides of ABC?

In this case AF = FB, BD = DC, and AE = EC, so AF/FB = 1, BD/DC = 1, AE/EC = 1 and their product equals 1. Ceva's theorem tells us that the lines AD, BE, and CF must be concurrent. We call the point P in this case the centroid.

Initially, we considered only points P that lie inside the triangle ABC, but ceva's theorem holds for points P outside of triangle ABC as well. Click hear to see a GSP sketch that illustrates the theorem for any possible point P.

Seeing that the theorem holds for P outside of ABC allows us to look at another special case of P.

What if D, E, and F are the feet of the altitudes of triangle ABC?

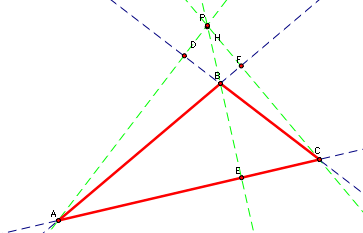
(1)

Triangle ACD is similar to triangle BCE

<BCE = <ACD -- same angle

<BEC = <ADC -- both right angles by construction

So, <EBC = <DAC

BC/AC = BE/AD = EC/DC

-------

(2) Triangle AFC is similar to triangle EAB

<FAC = <EAB -- same angle

<AFC = BEA -- both right angles by construction

So, <ACF = < EBA

AF/EA = CF/BE = AC/AB

-----

(3) Triangle BAD is similar to triangle FBC

<ABD = <FBC -- vertical angles

<ADB = <BFC -- both right angles by construction

So, <BAD = <BCF

AD/FC = AB/BC = BD/BF

-----

Multiplying (1), (2), and (3)

AF/EA * BD/BF *EC/DC= AC/AB * AB/BC *BC/AC

(AF * BD * EC)/ (EA*BF *DC) = 1

Now, by Ceva's theorems the lines are concurrent. We refer to the point p as the orthocenter.