Concurrency of Perpendicular Bisectors
By Mary
Negley
I want to prove that the perpendicular bisectors of
any triangle are concurrent.
Let
be any triangle, let D and E be the midpoints of
AB and BC, respectively and let l and m be
the perpendicular bisectors of AB
and BC, respectively. Let P be the point of intersection of l and m. The triangle is pictured below.
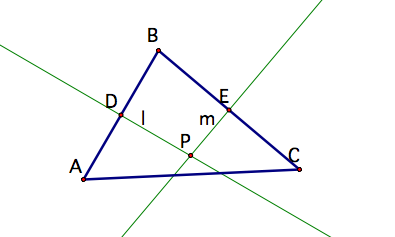
Now, make segments connecting P to each of the vertices of the triangle.
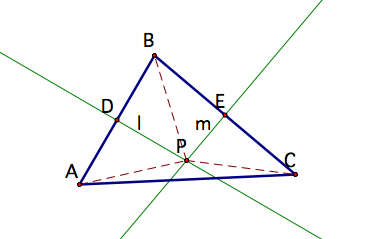
Notice that four new right triangles are formed (
, 
, 
, and 
). First look at
and 
. Since D is the midpoint of AB, AD = BD and since l
is the perpendicular bisector of AB,
and 
: so 
. By reflexivity
. So by SAS, 
. By definition
of congruent triangles, 
. Similarly, 
and
. Since 
and 
, by transference, 
.
Now look at 
. Since 
, 
. Let F be the midpoint of AC and make a segment between P and F.
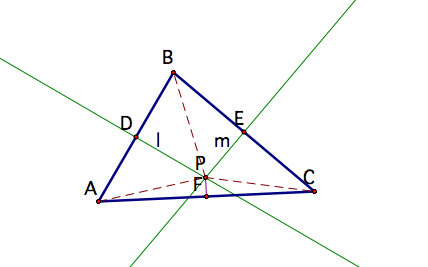
By
construction, 
. Since 
, 
, and 
, we have SAS, so 
. By definition of congruent triangles, 
. Since 
can be extended
to be a line, 
. So if 
, we find that:
Since 
, 
, so the segment connecting P to F
must be part of the perpendicular bisector of AC. I have
shown that this perpendicular bisector goes through P also.
Therefore, the perpendicular bisectors of 
are concurrent.