Concurrency of Angle Bisectors

By Thuy Nguyen

Theorem: The three angle bisectors of the internal angles of a triangle are concurrent.

To prove this we will need the following two theorems:

Hypotenuse-Leg Theorem: In a neutral geometry if ▲ABC and ▲DEF are right triangles with angles at C and F, and if segment AB is congruent to segment DE and segment AC is congruent to segment DF, then ▲ABC and ▲DEF are congruent.

Hypotenuse-Angle Theorem: In a neutral geometry, let ▲ABC and ▲DEF be right triangles with right angles at C and F. If segment AB is congruent to segment DE and the angle at A is congruent to the angle at D, then ▲ABC and ▲DEF are congruent.

Proof:

Let ▲ABC be any triangle. Let L be the line that bisects angle A and let M be the line that bisects angle C. Let P be the point where L and M meet. We claim that segment BP will bisect the angle at B, hence giving us our desired result. 

Now we drop perpendiculars from point P onto line AB, BC, and AC.

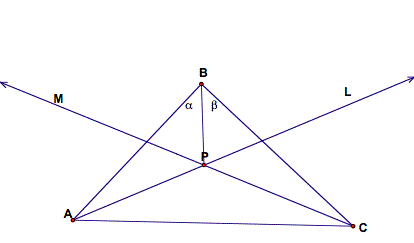
Then ▲AFP and ▲ADP are congruent triangles by the Hypotenuse-Angle Theorem. So we have that segments PF and PD are congruent. Also ▲CDP and ▲CEP are congruent triangles by the Hypotenuse-Angle Theorem, so segments PE and PD are congruent. Hence, segments PF and PE are congruent. By the Hypotenuse-Leg Theorem, ▲BFP and ▲BEP are congruent triangles. Therefore, angle a= angle b. QED.