Altitudes and Orthocenter

By Thuy Nguyen

 

Theorem:

Given triangle ABC, let H be the orthocenter and let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully. Then

 

 

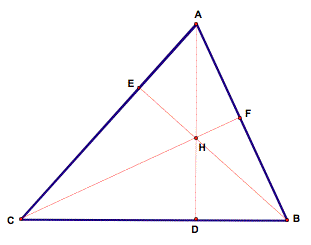
Proof:

 

Let

 

T = area of ABC

T₁ = area of HAB

T₂ = area of HBC

T₃ = area of HAC

 

Then we have

 

T = T₁ + T₂ + T₃

ð    (T₁ + T₂ + T₃) / T = 1

ð    (T₁ / T) + (T₂ / T) + (T₃ / T) = 1

 

But we also have that

 

T = ½ (AB)(CF) = ½ (BC)(AD) = ½ (AC)(BE)

T₁ = ½ (AB)(HF)

T₂ = ½ (BC)(HD)

T₃ = ½ (AC)(HE)

 

Hence T₁ / T = HF / CF, T₂ / T = HD / AD, and T₃ / T = HE / BE. So

 

(HF / CF) + (HD / AD) + (HE / BE) = 1.

 

Now note that:

 

AH = AD – HD

BH = BE – HE

CH = CF – HF

 

Substituting this into (AH / AD) + (BH / BE) + (CH / CF) we get

 

(AD – HD) / AD + (BE – HE) / BE + (CF – HF) / CF = 3 – [(HD / AD) + (HE / BE) + (HF / CF)] = 3 – 1 from previous result

= 2. QED.

 

Now in the case when triangle ABC is obtuse, the results no longer hold since the orthocenter H lies outside of our triangle. But if we consider the triangle HBC, then our orthocenter is at A and the results shown above will hold.

 

 

 

Return