Gregory Schmidt
Write-up #2
Parabolic Investigations
Problem: Produce 5 to 10 graphs of
on the same axes using different values for 
. Does varying 
change the shape
of the graph? What about the
position?
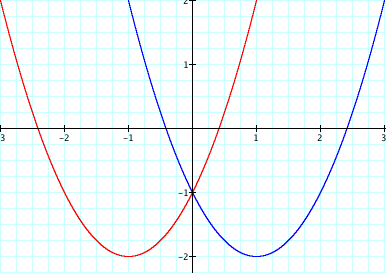
We will begin by considering our graph with 
. So let 
and
.
(1)
Now we notice that the two graphs both have the same
y-intercept of 
. But we need not
graph this in order to find the y-intercept of a graph of the form 
. Setting 
, we see that our graph will always have a y-intercept of 
. When we solve
for the x-intercepts of 
and 
, we see that they are 
and 
, respectively.
Hence, the x-intercepts of our graphs are symmetric about the
y-axis.
Finally, we see that 
and 
, both have a
vertex of 
and 
. As we will
see, all graphs of the form 
will have a
vertex of 
.
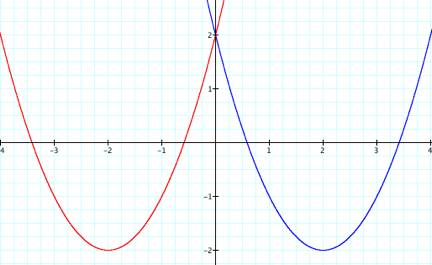
Let us now consider the graphs with 
, so that we have
and 
.
(2)
Again, we can graphically verify what we already now, and
that is that our y-intercepts are 
. These graphs have
the same shape as the previous two, and only differ by the x-intercept and
y-intercept. As previously
mentioned, we can see that 
and 
have a vertex of
and 
, respectively.
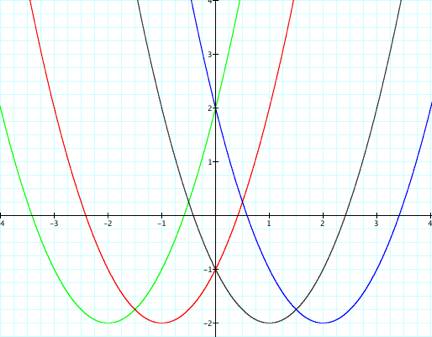
Graphing all of these at once we have:
(3)
All of these graphs are of the same class of graphs, which
is why they all appear so similar.
As we have seen, varying 
, merely changes the x-intercept, the y-intercept, and the
vertex, but leaves the overall shape of each graph unchanged.
This leads us naturally to question the shape and position of graphs of the form
.
What conclusions can one make based on the discoveries from the previous graphs?
Well, graphs of this form are certainly quadratic, and so
should have the same general shape as the previous graphs. Furthermore, setting 
, in order to determine the y-intercept gives us 
, which while different than before, is still quite similar
in its relation to 
and 
. Finally, we
see that graphs of this form have a vertex of 
.
Let us consider an example. Take 
. So we have
and 
.
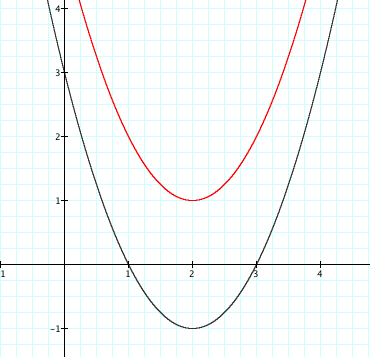
(4)
If we desired to reflect these graphs about the y-axis, we
now see that we can do so by considering graphs of the form 
.
Again let us consider for 
. So we have:
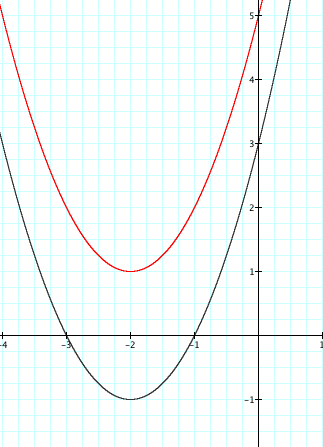
(5)
Notice there is no difference in the shape of these graphs.
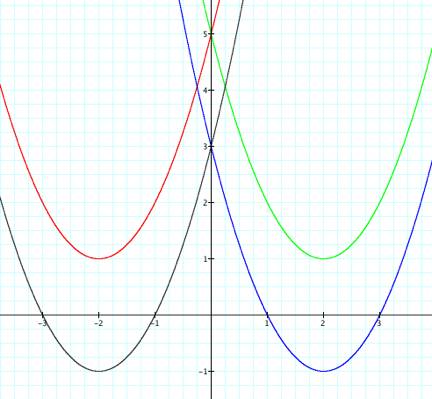
(6)
In fact, all of the graphs we have consider thus far have the same shape, and differ only with respect to their intercepts on the xy-axis, as well as their vertices.
Notice:
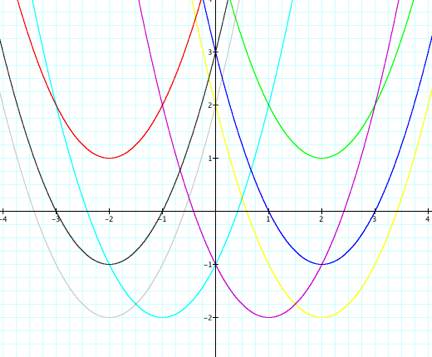
All of the graphs we have seen here of the same class of graphs, namely quadratic forms.
