Parametric Curves

Problem: Write parametric equations of a line segment through (7,5) with slope of 3. Graph the line segments using your equations.

Recall the point-slope form for the equation of a line is .

If I let x=t, then and we obtain the parametrization

.

I can obtain another parametrization for the line if I let

In this case and I have

I know that a pair of parametric equations is a pair of continuous functions that define the x and y coordinates of a point in a coordinate plane in terms of a third variable, such as t, called the parameter.

Thus, a parametric curve in the plane is a pair of functions

x= f(t)

y= g(t)

where the two continuous functions define ordered pairs (x,y).

So my substituting into: we get:

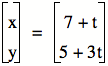
Now, let’s check this out. When I put these back into point-slope form I obtain the following:

y-5 = 3(x-7)

y=3x - 21 + 5

y=3x-16

Now, let’s see if our calculations are correct.

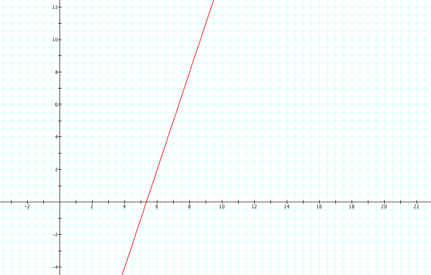
Let’s graph y=3x-16

Now, let’s graph 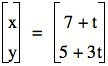and pray that it’s the same graph.

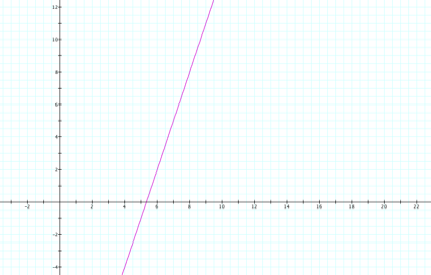
Yes, both graph the same line, so my calculations were correct.