Quadratic Functions

I will examine the standard equation, , and the effect of different values of a, b, and c on its roots.

Let y = ax^2 + x+ 1. The following shows the graph of this function when b and c remain constant while a varies.

a = 3, 2, 1, 0, 1, 2, 3

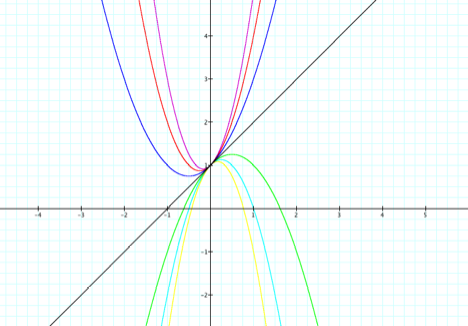
In all cases, the graph intersects the y-axis at y=1. When a>0, this function has no real roots because the function opens up. However, when a<0, the function has two real roots, because the function opens down and when a=0, the function has one real root. Also, if we imagine a starting from 0, then as the value of a increases, the parabola gets more narrow and as a decreases the function gets wider. Of course, the number of roots will change depending on if the vertex is above or below the x axis.

Now, let y=x^2 –x + c and let’s see what happens when a and b remain constant and c is varied. c=3, 2, 1, 0, -1, -2, -3

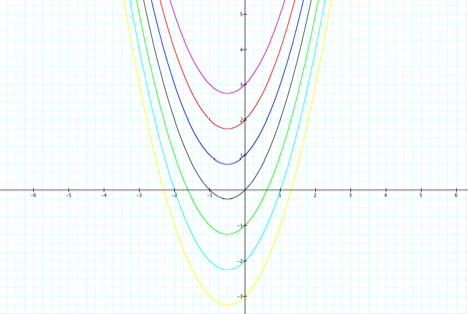
Notice that when c=0 or c>0, this function has two real roots. If c=0, one of its roots is zero and the other is -1. If c >0, one of its roots is negative and the other is positive.

Finally, let y=x^2 +bx+1. The following shows the graphs of functions when a and c are constant, but b varies. c= 3, 2, 1, 0, -1, -2, -3

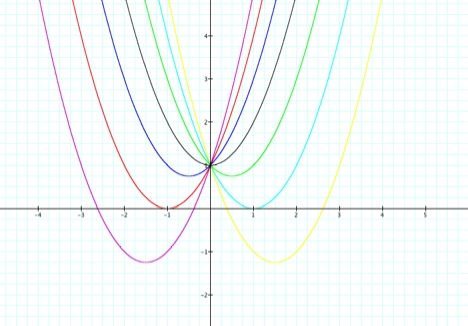
It looks like, when |b| =2, that the function will have only one root. When |b|>2, the function will have two real roots and when |b|<2 , the function will have no real roots.

Let’s consider the locu of the vertices of the set of parabolas graphs from y=x^2 +bx +1. Notice that the graph of this set of vertices is the parabola y=-x^2+1.

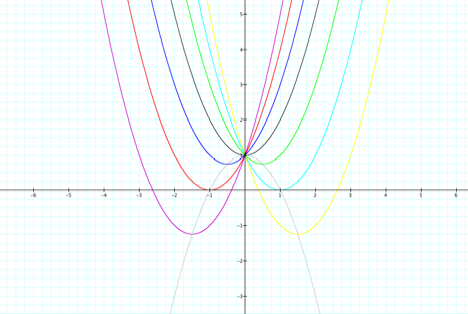
What about if a is negative, for the same values of b?

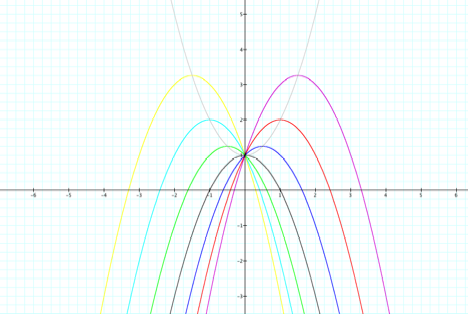
Notice this time that the graph of this set of vertices is the parabola y=x^2+1.

Now, I can generalize that the set of vertices of all parabola of the form y=x^2+bx+c, is the parabola, y=-x^2+c.