
Summer Tuggle
Assignment
3
Explore
y= ax2 + bx + c
when
a and c are constant and b changes
Quadratics are polynomials of
the second degree. The word “quadratic”
seems to imply a connection to the number four.
This is not so. Quad refers to the classic math problem
of trying to find a square with the same area as a given circle. This is called finding the quadrature of a circle.
Quadratic, therefore, refers to finding the area (x2) of a
square with a side length of x.
The standard form of a quadratic is y= ax2 + bx + c. The graph of
a quadratic is a curve that is referred to as a parabola. Let’s explore what happens when a and c are constant and b is changed.
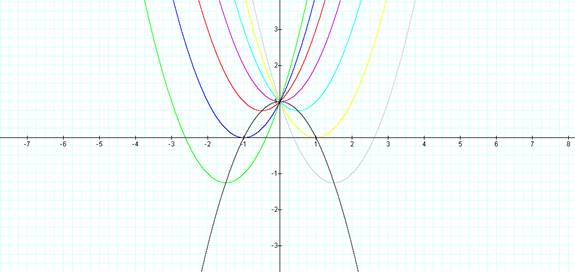
Below is the graph of parabolas that have different “b”
values. Specifically b= 0, 1, 2, 3, -1, -2, -3
All of the parabolas intersect the y-axis at 1. When b is less than 0 the parabola’s vertex
is in the 1st or 4th quadrant of the coordinate plane
(the aqua, yellow and gray curves). When
b is greater than 0 the vertex falls in the 2nd or 3rd
quadrant (red, blue, and green curves).
The purple curve, whose vertex falls directly on the y-axis, has a b of
0. It is interesting to note that all
the vertices fall on a specific curve (the black curve).
Since we know that the x coordinate of a parabola can be
found using (-b/2a) and we know that in this case a=1 we can solve for b
X=![]()
2x = -b
-2x = b
Now take this a plug it into our standard formula where a
and c are 1, but b is constant y=x2 + bx +
1
y=x2 + (-2x)x + 1
y= x2 -2x2 + 1
y=-x2 +1
Therefore all the vertices will fall on the curve y=-x2
+1.