
FRIDAY THE 13th
Friday the 13 has become one of the most feared days of the year for the more suspicious ones, but unlike Halloween every year brings a different amount of Friday the 13ths. So how can we prepare ourselves at the beginning of the year for how many unlucky Fridays we will have?First let's see if in fact every year we are guaranteed to have a Friday the 13th. We know that every week has seven days in it so for this problem let us work in mod 7. So let Sundays, the first day of the week, be represented by a 0, Monday by a 1, Tuesday by a 2, Wednesday by a 3, Thursdays by a 4, Fridays by a 5 and Saturdays by a 6. Then the next Sunday will once again be a 0.
In order to see if Friday the 13th will happen at least once in a year I set up an excel spreadsheet that represents all the days of the 12 months and I let the year start out on a Monday, hence using a 1. Let us take a look at what I came up with:
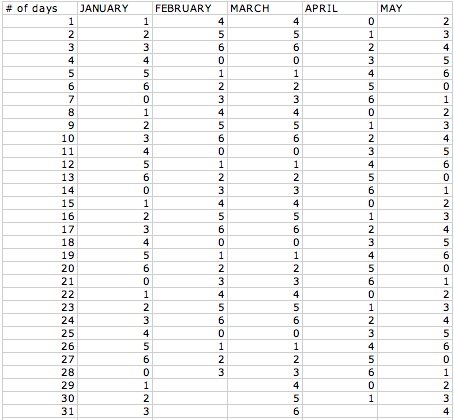
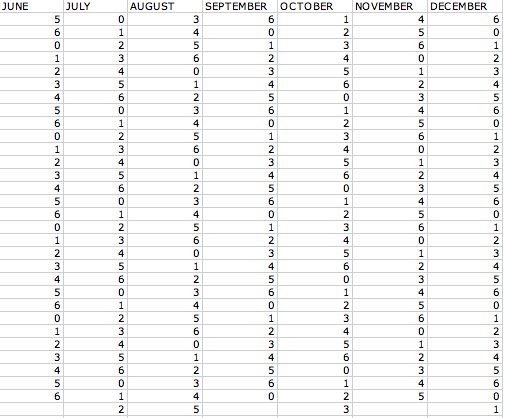
Now looking at our first column we can look at the row that follows the number 13. So let us look at each number that came up in the slot for the 13th each month:
January-6, February-2, March-2, April-5, May-0, June-3, July-5, August-1, September-4, October-6, November-2,
December-4
Looking at our numbers we have one number one, three number twos, one number three, two number fours, two number fives, two number sixes, and one number 0. So we can set up a table for which days the 13th will fall on and how many times it will happen:
1st day(Monday)-1
2nd day(Tuesday)-3
3rd day(Wednesday)-1
4th day(Thursday)-2
5th day(Friday)-2
6th day(Saturday)-2
7th day(Sunday)-1
What would happen if the year started out on a Tuesday? Let's set up an excel sheet and check it out.
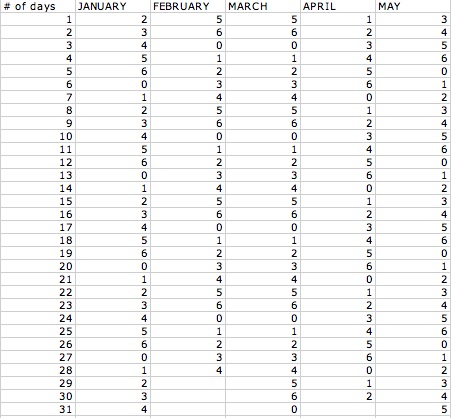
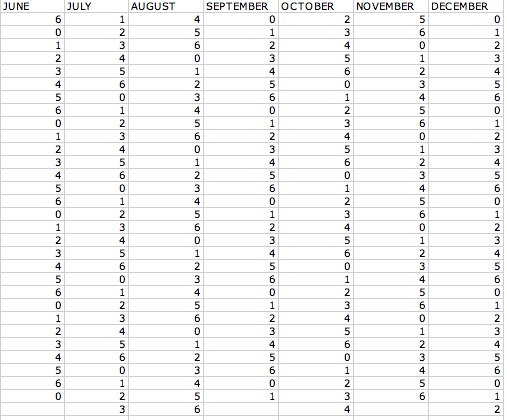
Let's see what days the 13 falls on for when our year starts out on Tuesday:
January-0, February-3, March-3, April-6, May-1, June-4, July-6, August-2, September-5, October-0, November-3
December-5
So for this set up we can form another table and see what we get. Although this time we will start on a Tuesday.
1st day(Tuesday)-1
2nd day(Wednesday)-3
3rd day(Thursday)-1
4th day(Friday)-2
5th day(Saturday)-2
6th day(Sunday)-2
7th day(Monday)-1
Could we possibly have a pattern. From the two different excel sheets, the pattern I see so far is that whatever the first day we start the year out with, the 13 will occur on that day once, the second day of the year the 13th will occur three times, the third day of the year the 13 will occur on that day once, the fourth day the 13th will occur on that day twice, the fifth day of the year the 13th will occur on that day twice, on the sixth day the 13th will occur on that day twice and whatever day is the seventh day of the year is the 13th will occur once on that day. So let's check our thinking with one more excel sheet. Let's let the first day of the year be a Friday and so we will start with the number 5.
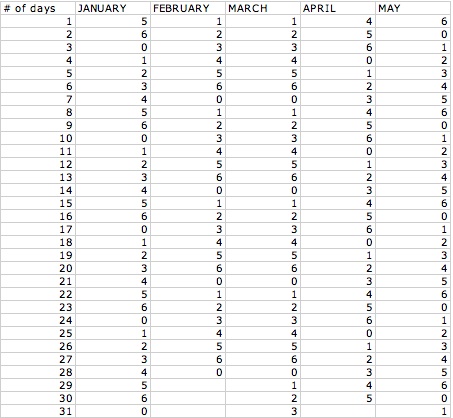
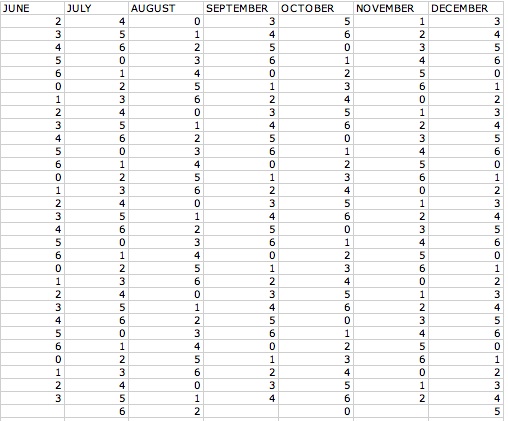
Let's see which days the 13 falls on when we start our year out at on a Friday.
January-3, February-6, March-6, April-2, May-4, June-0, July-2, August-5, September-1, October-3, November-6
December-1
So this forms the following table:
1st day(Friday)-1
2nd day(Saturday)-3
3rd day(Sunday)-1
4th day(Monday)-2
5th day(Tuesday)-2
6th day(Wednesday)-2
7th day(Thursday)-1
Does this check in with our original pattern?
YES IT DOES! So it is fair to say that the least a number, or day of the week, is represented is once and the most frequent is three times. With this we can conclude that the minimum number of times we will experience a Friday the 13th would be once and the maximum amount of Friday the 13ths would be three. When would these occur you wonder? Well let's take a look. In order for the 13th day to end up at the 3 slot we would have to start out on a Thursday because with the pattern it is the second day of the year that will have three 13ths to their name! So what days will we have to start out with to have only one Friday the 13th? Here we would have three different days since 1 occurs in our pattern three times. If the year starts our with a Wednesday, a Friday or a Saturday we would only have one Friday the 13th!
Click HERE for a spread sheet for a leap year(it is on the second sheet),so that you can form your pattern and see what days we must watch out for.
Now have you ever wondered if it is possible that we could have two Friday the 13ths back to back? Let's once again take a look:
Looking closer at our lists of when Friday the 13th occurs in each month notice that February and March both always have the same day for the 13th. In the spreadsheet for starting the year off on a Monday the 13th will occur on Tuesday for both months. And if we take an even closer look we can see that all of the days in February match the dates in March. If February starts on a Tuesday so will March! Why is this you may wonder. Well, for a non leap year February has 28 days in it which happens to be a multiple of 7, 7 can go into 28 four times without a remainder so the month of February will complete four whole cycles in mod 7. So if February starts on a Wednesday then it will end on a Tuesday and March will pick up on a Wednesday. So no matter what the 13th will occur on the same day in February and March, so when February has Friday the 13th so will March. Can this happen for any other months? No! Since all other months end in 30 or 31 days, which are not divisible by 7, no other two months will both have Friday the 13 consecutively.
What about a leap year? For a leap year February will have 29 days instead of 28 and so it will no longer be divisible by 7. So it will go through 4 cycles and a new one will start with out finishing. So for a leap year no months are divisible by 7 and hence, leap years will never have two consecutive Friday the 13ths.
In conclusion what out for years that start out on a Thursday! (They must be non leap years of course.)