

ASSIGNMENT 7
TANGENT CIRCLES
BY:
DEBORAH ECKSTEIN
Assignment 7 is an exploration of tangent circles. First let's make a script tool so that we can easily obtain tangent circles in GSP if we so please.
First, construct a circle and then put a smaller circle inside the first circle. I will now construct a circle tangent to these two circles!!!
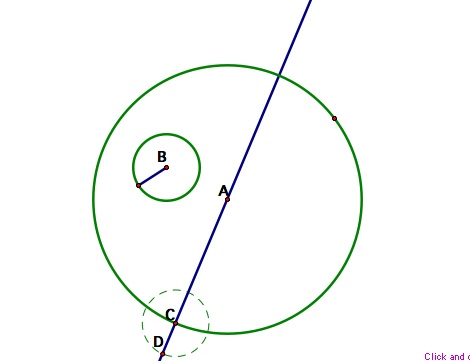
Label the center of our big circle A, the center of the smaller circle B and then label any point on circle A C.

Now construct a line that goes through the points A and C. Then taking the radius of our smaller circle construct a circle about point C that has the same radius and label its intersection with AC point D.
Then connect point B to point C and using the new segment construct its midpoint and at that midpoint construct a perpendicular bisector to that line.

Next label the intersection of line AC to the perpendicular bisector E. E will become the center of our tangent circle and the radius will be the distance from E to point C. We now have our tangent circle (It is the RED circle).

Here is the script tool for this construction...TangentCircles!
Here is an animation of the tangent circles...Animation! Notice that no matter where we move the point C, our circle remains tangent to the two original circles. Now let's trace the center of our constructed tangent circle...Traces! Notice that when we trace the center of our tangent circle we get an ellipse!
Now let's look at a different case where we have the two circles intersecting. We will use our created script tool to make the construction.

Here is an animation of these tangent circles with the center of our tangent circle being traced...Animation! Notice that our locus is an ellipse.

Now let's look at another case where the two circles are disjoint. We will once again use our script tool to make our construction.

Now once again trace the center of our tangent circle and notice that it creates a hyperbola, which is our locus!

Here is an animation of the tangent circles creating the hyperbola Animation.