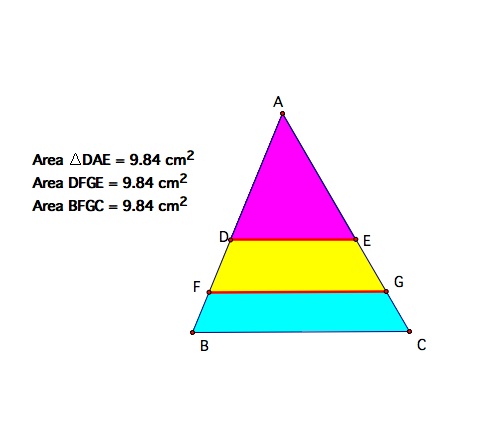
For this exploration of the trisection of the area of a triangle we are going to find where two parallel lines need to be placed inside a triangle such that the area of the triangle is trisected.
So we will define our problem as:
Given a triangle ABC, construct two line segments parallel to the base BC to divide the triangle into three regions with equal areas.
Now we need to find out where to put the two line segments FG and DE so that they will be parallel to BC and trisect the area of the triangle.
So we can look at the triangle and imagine that we would have three individual triangles within triangle ABC. So we would have,

So let us define the areas of these three triangles (given arbitrary heights):
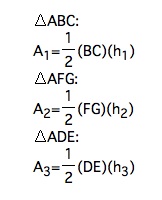
Let us first try to find the length of the segment FG.

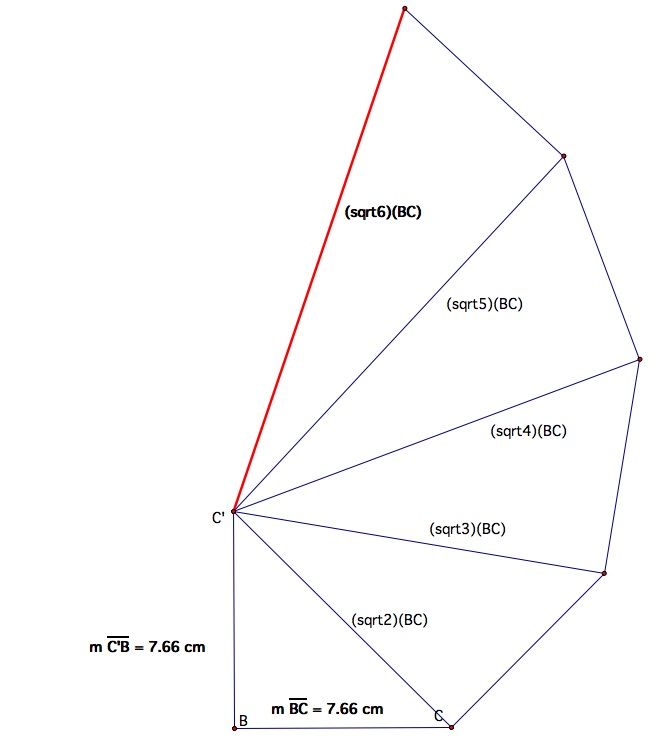
Now we have to take the segment (sqrt6)(BC) and trisect it to get (sqrt6/3)(BC) .
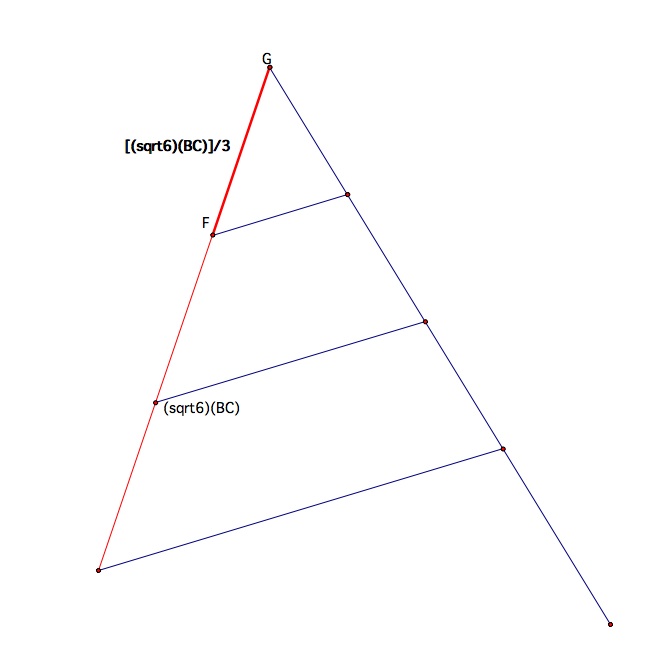
We can take the constructed length and put it inside of triangle ABC so that it is parallel to BC.
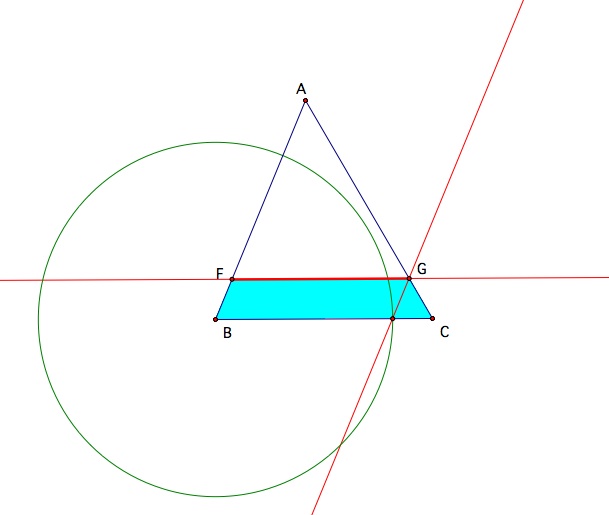
Now we need to find the placement of our last segment DE.

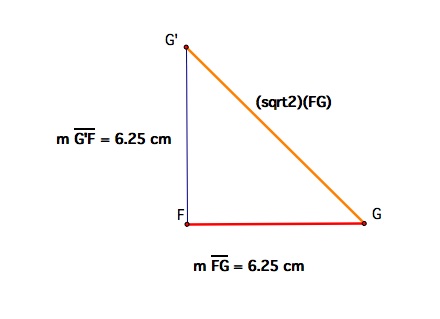
Now we can take the segment (sqrt2)(FG) and bisect it to get the segment length we need.
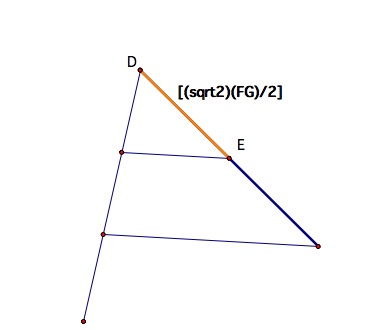
Take the constructed length and put it inside of triangle ABC so that it is parallel to BC and FG.
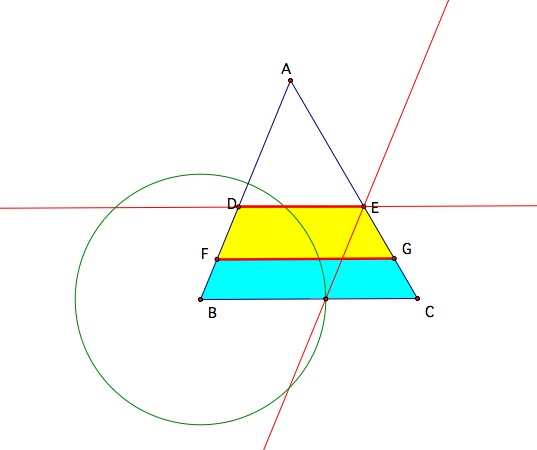
We now have the placement of both segments so let's calculate the area of our three sections: