We
are going to consider a situation where Barney moves in and around a
triangle according to some rules. Barney must always move
parallel to a side of a given triangle. He moves until he hits a
wall, but then must stop and move parallel to a different side of the
triangle. The object is to figure out if Barney will return to
his starting point, how many walls he will contact in the process, and,
if possible, to determine something about the length of his path. So,
let's get Barney bouncing. The picture below should give you the
idea of how Barney gets around.
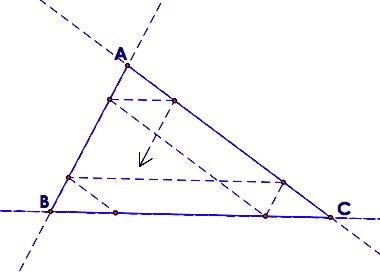
First, let's consider the path if Barney begins on a side of the triangle.
Click here for a GSP file to move Barney around to determine the number of walls that Barney will contact on his trip. Try to find the answer yourself before you click on the answer box.
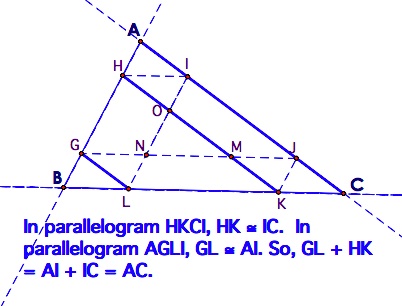
What if Barney starts on the midpoint of a side? In the diagram below, he begins in the middle of side BC. In this case we can figure out how many walls he will contact and what the length of his path will be relative to the perimeter of the original triangle. The explanation is below.
If Barney starts at a random point in the interior of the triangle,
he will find himself completing the same trip as if he had begun on the side, as shown in this figure. 
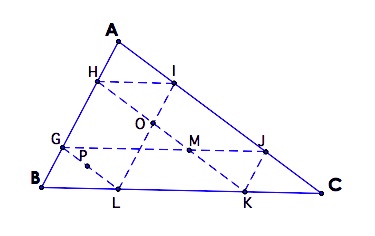
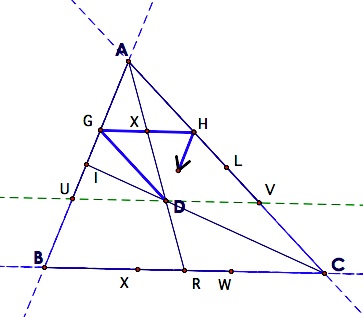
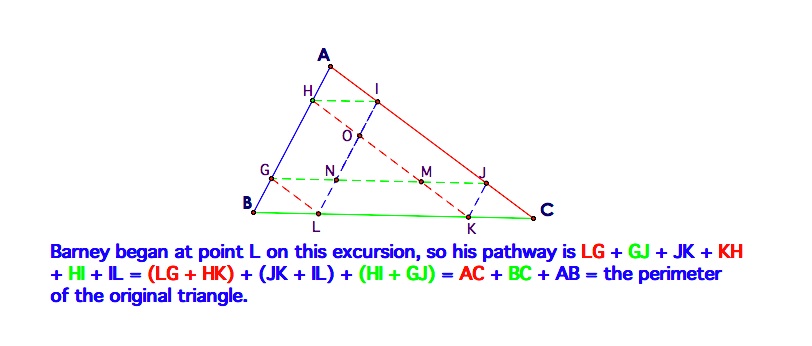
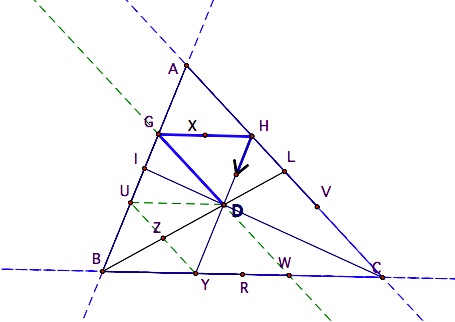
If Barney starts at the centroid, the point of concurrency of the medians, he has an even shorter path. He again returns to this starting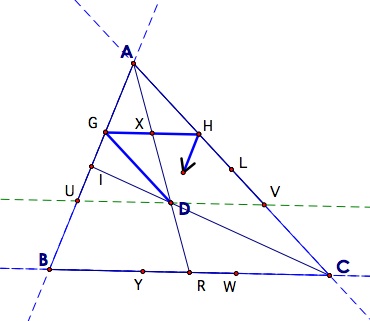
point after hitting the second wall. The path that he has
traveled makes a congruent triangle to AGH, since each triangle is half
of the parallelogram AGDH. This path appears to be 1/3 of the
perimeter of triangle ABC. We'll see if we can prove this.
The details for each of the three parts are found below.
Part 1:
Part 2:
Part 3:
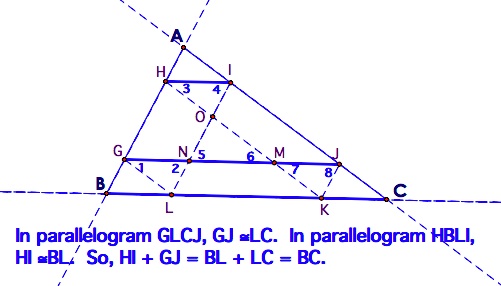
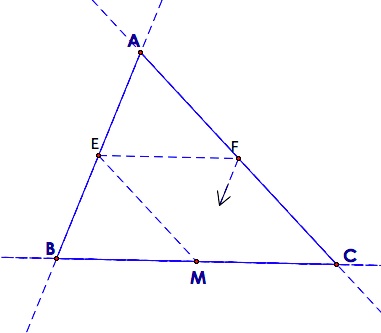
Now, what if Barney strays to the outside of the triangle? He would follow a path like the one shown in this figure.
Obviously,
Barney covers a distance of more than the perimeter of the original
triangle. Could we figure out what distance he covers relative to that
original perimeter?
In the following explanation, I have analyzed the distance that Barney is covering, but the results were not very satisfying. However, the result does give a way to determine the length of Barney's path based on the following:
the three sides of the original triangle
the altitudes of the original triangle
the distance Barney's pathway is from each of the three sides.
So, consider the diagram below and explanations below.
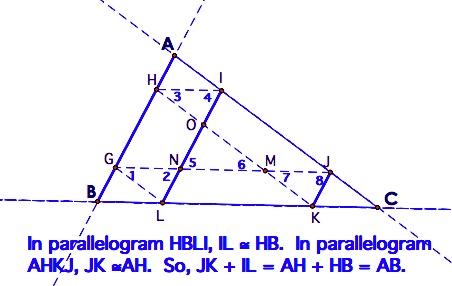
That takes care of the right triangles, so now we will consider the other three yellow triangles on the vertices of triangle ABC.
We need the picture again.
First, let's consider the path if Barney begins on a side of the triangle.
 | ||
 |  |  |
 | ||
Click here for a GSP file to move Barney around to determine the number of walls that Barney will contact on his trip. Try to find the answer yourself before you click on the answer box.
What if Barney starts on the midpoint of a side? In the diagram below, he begins in the middle of side BC. In this case we can figure out how many walls he will contact and what the length of his path will be relative to the perimeter of the original triangle. The explanation is below.
 |  |
If Barney starts at a random point in the interior of the triangle,
he will find himself completing the same trip as if he had begun on the side, as shown in this figure. If Barney starts at the centroid, the point of concurrency of the medians, he has an even shorter path. He again returns to this starting
point after hitting the second wall. The path that he has
traveled makes a congruent triangle to AGH, since each triangle is half
of the parallelogram AGDH. This path appears to be 1/3 of the
perimeter of triangle ABC. We'll see if we can prove this.The details for each of the three parts are found below.
Part 1:
Part 2:
 | |
 | |
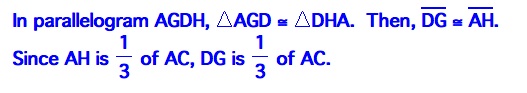Part 3:
 |  |
 | |
Now, what if Barney strays to the outside of the triangle? He would follow a path like the one shown in this figure.
In the following explanation, I have analyzed the distance that Barney is covering, but the results were not very satisfying. However, the result does give a way to determine the length of Barney's path based on the following:
the three sides of the original triangle
the altitudes of the original triangle
the distance Barney's pathway is from each of the three sides.
So, consider the diagram below and explanations below.
| NOTE
before we begin: Angles that are congruent due to easily seen
relationships have been marked in the diagram, but the explanations
have been omitted to save space (and to avoid annoying the reader).
As Barney travels along the parts of his path, PF, IJ, and MN, he covers the same distance as the perimeter of the original triangle, or AB + BC + AC, since PF, IJ, and MN are opposite sides of rectangles from the three sides of the triangle. So, we need to add in the distances he covers as he goes around the yellow portions of this diagram. Se will start with the right triangles below BC.  |  |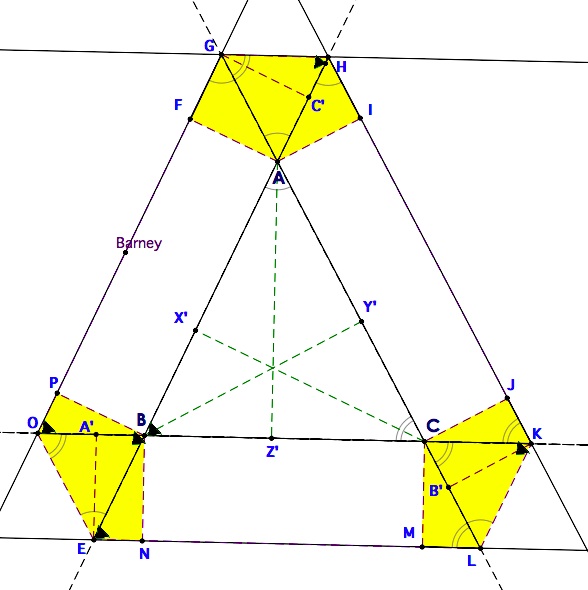
 | |
 |
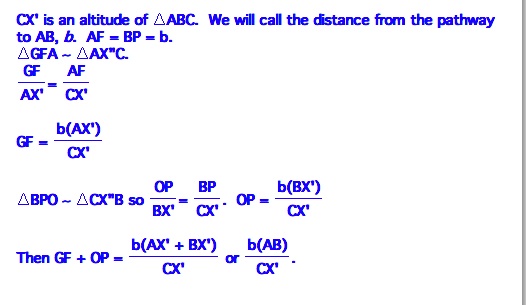That takes care of the right triangles, so now we will consider the other three yellow triangles on the vertices of triangle ABC.
We need the picture again.
 | |
 | |
 |
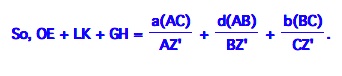