Centers of a Triangle Ruff

An Investigation of Centers of a Triangle
by
Jackie Ruff

There are several important points where lines related to triangles meet. These are pictured below with brief descriptions.


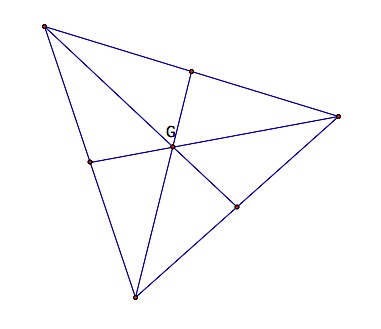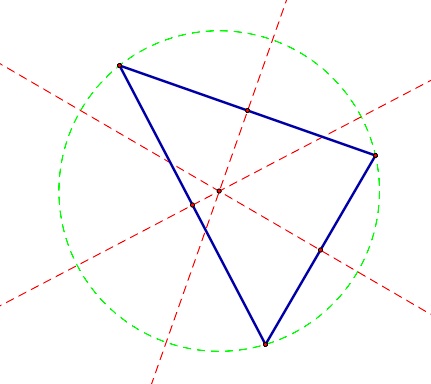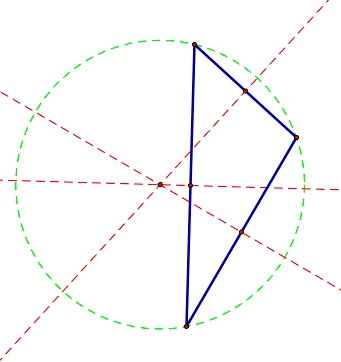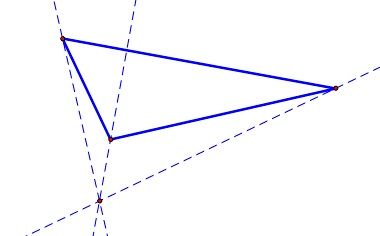
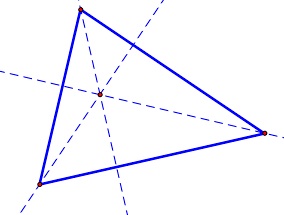
In the triangle above, point G is where the three line segments connecting each vertex to the midpoint of the opposite side intersect. This point is called the centroid.	The point where the three red lines meet in the diagram above is called the circumcenter. This is the point where the lines containing the perpendicular bisectors of the sides of the triangle intersect. It may be inside the triangle as in the picture above or ...	it may be outside of the triangle as shown above. Then using the distance from this point to any of the vertices of the triangle as the radius, the circle that circumscribes the triangle may be drawn.


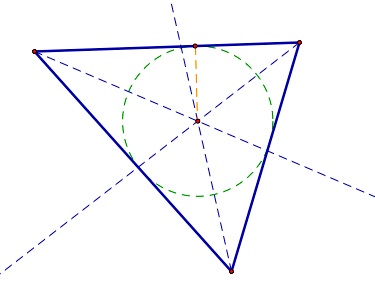The point where the angle bisectors intersect is shown in the diagram above. Since this point is equidistant from the two sides of each angle, it is equidistant from all three sides of the triangle. So, by using that distance as the radius, we can draw the circle that is inscribed in the triangle using the incenter as its center.	The point where the lines containing the altitudes of the triangle meet is shown in the triangle above. If the triangle is obtuse, the orthocenter will be in the exterior of the triangle and ...	if the triangle is acute, the point of intersection of the altitudes will be in the interior of the triangle.

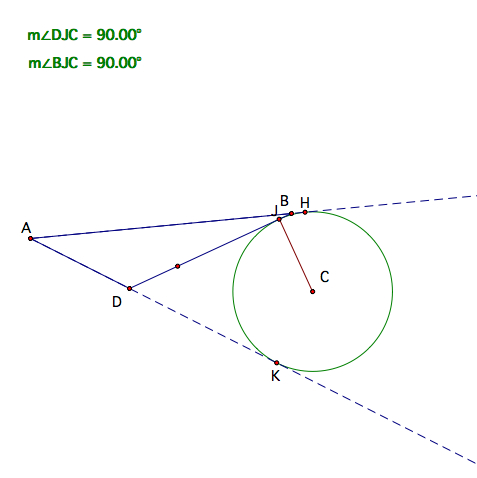
Next we will look a little more closely at a property of the angle bisectors. Not only are the angle bisectors of the three angles of a triangle concurrent at the point we call the centroid, but each angle bisector is also concurrent with the angle bisectors of the two opposite exterior angles of the triangle. A diagram and the proof are given below.

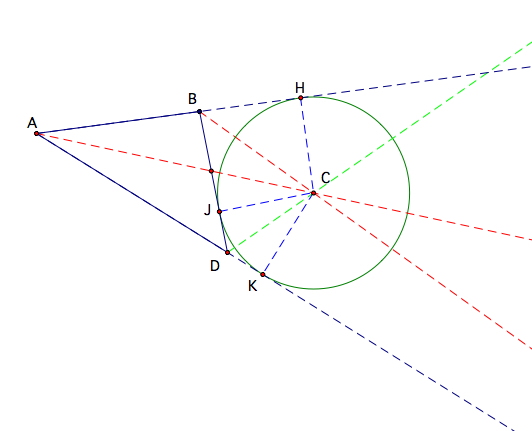
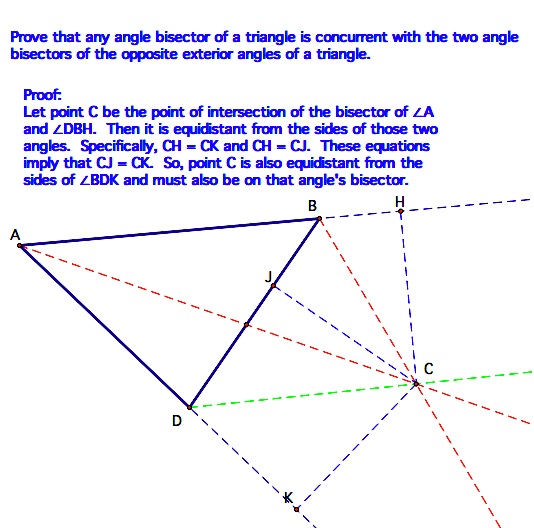	Once we see that this point is equidistant from the lines containing the three sides of the triangle, it is clear that it would be the center of a circle in the exterior of the triangle that is tangent to the triangle. An additional diagram is given below showing that this remains true when the shape of the triangle is changed.