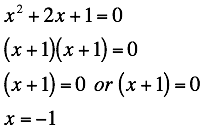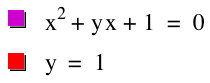---

Exploring Quadratics

By

Tonya DeGeorge

---

In this investigation, we will be looking at quadratics again, but in a different way. We will be looking at the following equation:

This graph will show the relationship in the (x, b) plane.

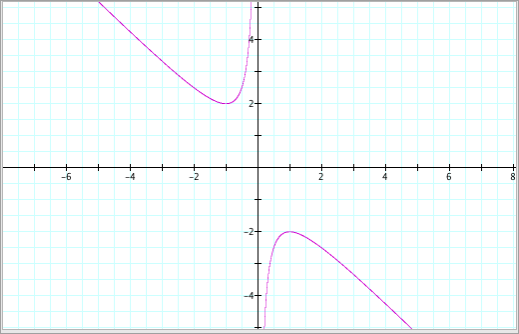
By adding a horizontal line in the (x, b) plane, it the intersection of the two graphs corresponds to the roots of the equation for a particular value of b. For example, suppose b = 2, we get the following graph:

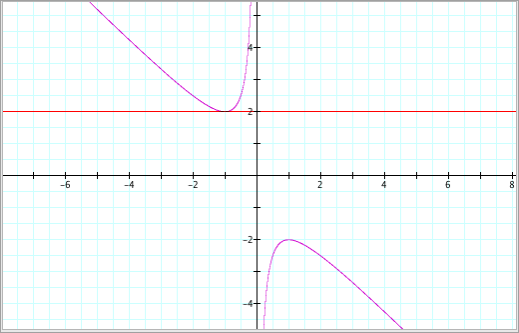
If we were to solve the equation by hand, we would find:

This corresponds to the graph above because the two graphs intersect at the point (-1,0) where x = -1. So how can we generalize this for different values of b? There are a number of cases to consider:

Case (i): b > 2

Case (ii): b = 2

Case (iii): -2 < b < 2

Case (iv): b = -2

Case (v): b < -2

Let’s look at these different regions. We’ve already seen what happens when b = 2. We found that there exists one double root: x = -1. For Case (i), where b > 2, lets choose b = 5. We find the following:

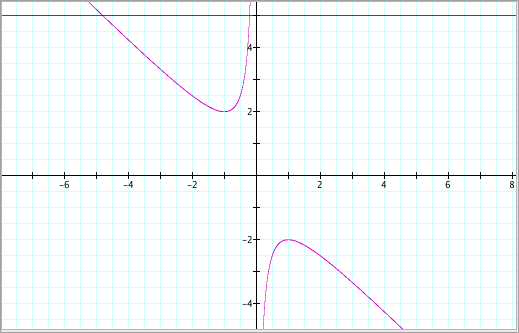
This implies that the equation has 2 negative roots. Let’s check this by looking at the equation:

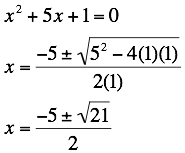
Therefore, we see that there exists 2 negative real roots.

Below are summaries for the next three cases:

For Case (iii), where -2 < b < 2, let’s choose the value b = 1. We find:

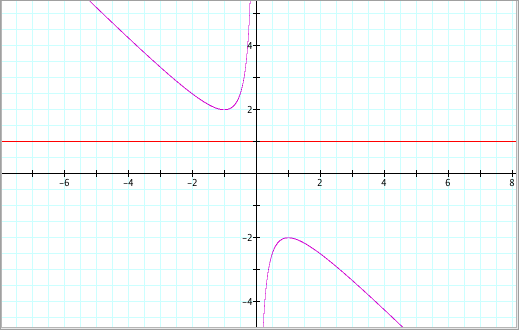
There are two imaginary roots (hence, the line does not intersect the graph).

For Case (iv), where b = -2, we get:

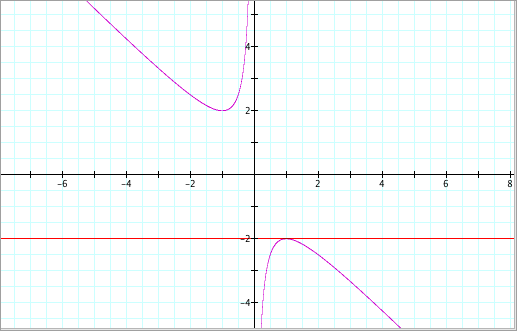
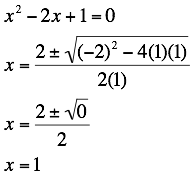
There is one repeated root at x = 1 (where the graph intersects at one point).

For Case (v), where b < -2, let’s choose b = -4. We find:

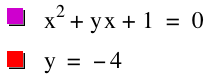
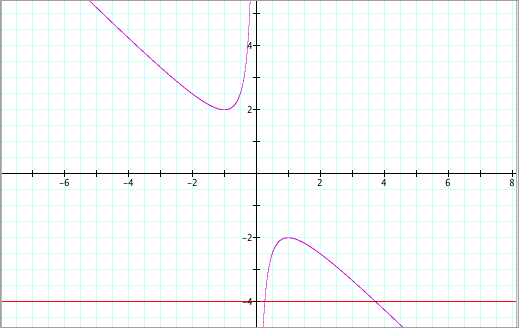
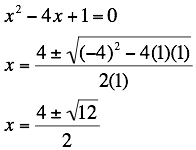
There exists two positive real roots.

In conclusion, we find:

Values of b	Types of roots
b > 2	Two negative real roots
b = 2	One double root (x = -1)
-2 < b < 2	Imaginary roots
b = -2	One double root (x = 1)
b < -2	Two positive real roots

Now suppose we look at the value of c and change it to -1 and compare what happens to the graph when this change is done.

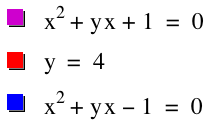
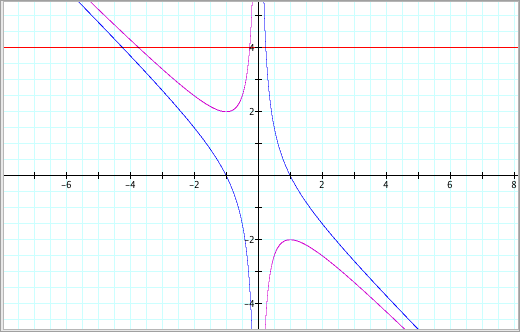
As we can see, when we change the value of c to -1, the graph changes into a hyperbola. What happens when we use other values of c? Let’s use the following values:

c = -2, -1, 0, 1, 2 (all on the same graph):

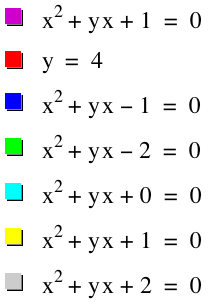
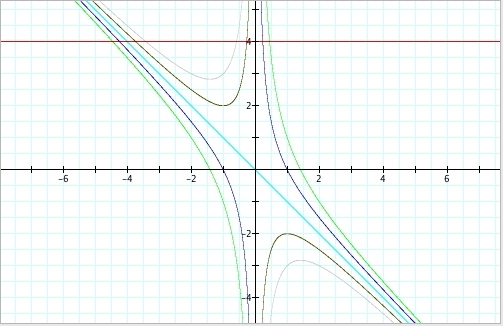
From here, we can see that the value of c changes the graph in three different ways. It could be a hyperbola (two different types) or a line. The three cases seem to be:

Case 1: when c < 0: hyperbola (asymptotic to x = 0 and y = -x)

Case 2: when c = 0: a line (y = -x)

Case 3: when c > 0: a hyperbola (asymptotic to x = 0 and y = -x)

*Note that the hyperbola is restricted to different areas of the plane depending on the value of c.

---

Return

---