

Assignment 1:
Exploring Asin(Bx+C)+D
by
Margo Gonterman
Periodic Function
A periodic function is a function, such as sin(x), that repeats its values in regular intervals
Sin(x) oscillates, or goes back and forth, between its maximum and minimum value
Amplitude
The amplitude of the graph is the maximum height the graph reaches from the x-axis
Period
The period is the distance along the x-axis that is required for the function to make one full oscillation
Phase Shift
The phase shift is the measure of how far the graph has shifted horizontally
Vertical Shift
The vertical shift is the measure of how far the graph has shifted vertically, either up or down, from its initial position
Let's examine the graph of y=sin(x).
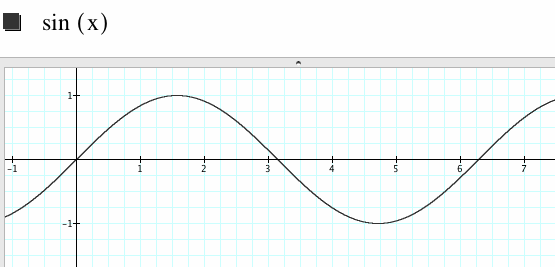
The graph of y=sin(x) has:
- an amplitude of 1
- a period of 2pi
- a phase shift of 0
- a vertical shift of 0
Let's look at what happens as A varies
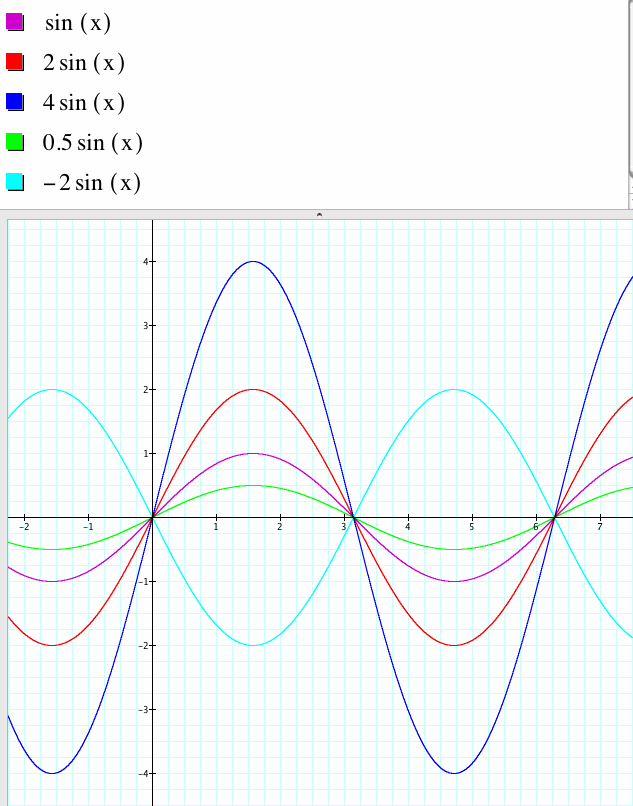
When A=1, the graph has an amplitude of 1.
As A increases increases from 1, the amplitude of the graph increases. For example, when A=2, the amplitude of the graph is 2 and when A=4, the amplitude of the graph is 4.
When A=1/2, the amplitude of the graph is 1/2.
When A is negative, the amplitude is the absolute value of A and the graph is reflected across the x-axis. For example, when A=-2 the graph is a reflection across the x-axis of y=2sin(x).
When A is zero, the graph degenerates to y=0 or a line that lies on the x-axis.
Thus, the absolute value of A is the amplitude of y=Asin(Bx+C)+D. When A<0, the graph is reflected across the x-axis.
Let's look at what happens as B varies

When B=1, the graph has a period of 2pi.
When B=2, the graph has a period of pi.
As B increases from 1, the period decreases.
When B=1/2 the period of the graph is 4pi.
When B<0, the graph is the reflection across the y-axis and the period remains positive. For example, when B=-2, the graph has a period of pi and is a reflection across the y-axis of y=sin(2x).
When B=0, the graph degenerates to a line on the x-axis.
The period of the graph is |(2pi)/B|.
For B>0, as B increases, the period of the graph decreases.
For B<0, as B decreases (becomes more negative), the period of the graph increases.
In general, as the absolute value of B increases, the period of the graph decreases.
Let's look at what happens as C varies

When C=0 the graph has a phase shift of zero.
When C=1, the graph shifts to the left by one unit.
When C=2, the graph shifts to the left by two units.
When C=1/2, the graph shifts to the left by 1/2 unit.
When C=-1, the graph shifts to the right by two units.
When C is greater than zero, the graph shifts to the left. When C is less than zero, the graph shifts to the right.
It looks like C controls the phase shift, but let's see what happens when B is not equal to 1.

When B=3 and C=-2, the phase shift is 2/3 unit to the right.
When B=-2 and C=2, the phase shift is 1 unit to the right.
When B=.5 and C=-2, the phase shift if four units to the right.
The phase shift is equal to -C/B units.
Let's look at what happens as D varies
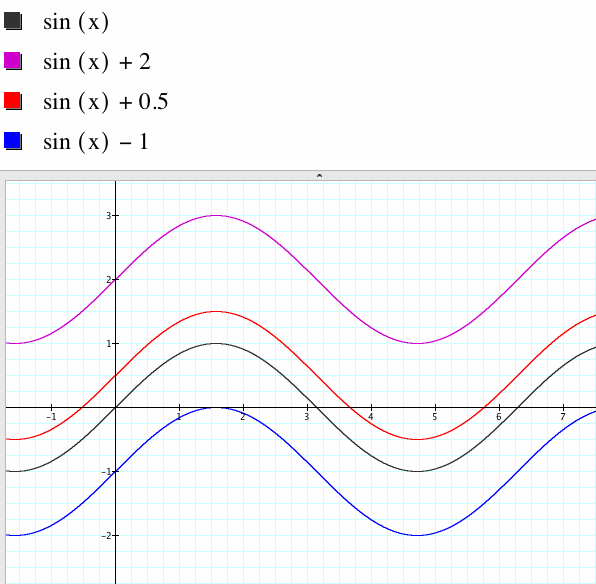
When D=0, the vertical shift is 0.
When D=2, the vertical shift is up 2 units.
When D=1/2, the vertical shift is up 1/2 unit.
When D=-1, the vertical shift is down 1 unit.
When D>0, the graph shifts up by D units.
When D=0, the graph does not shift up or down.
When D<0, the graph shifts down by D units.
In general, the vertical shift of the graph is D units.
Summary
y=Asin(Bx+C)+D
Amplitude: A (absolute value)
Period: (2pi)/B
Phase Shift: -C/B
Vertical Shift: D