Assignment 10:

Parametric Lines

by

Margo Gonterman

Goal:

Write parametric equations of a line segment through (7,5)

with a slope of 3.

What are parametric equations?

Instead of defining y in terms of x, parametric equations define both x and y in terms of a parameter t.

Each value of t yields a point (x(t),y(t)) that can be plotted.

The collection of all points for the possible values of t yields a parametric curve that can be graphed.

Step 1: Write an equation for a line through (7,5) with a slope of 3.

Point-Slope Form

y-y1=m(x-x1)

where (x1,y1) is a point on the line

and m is the slope of the line.

y-5=3(x-7)

y-5=3x-21

y=3x-16

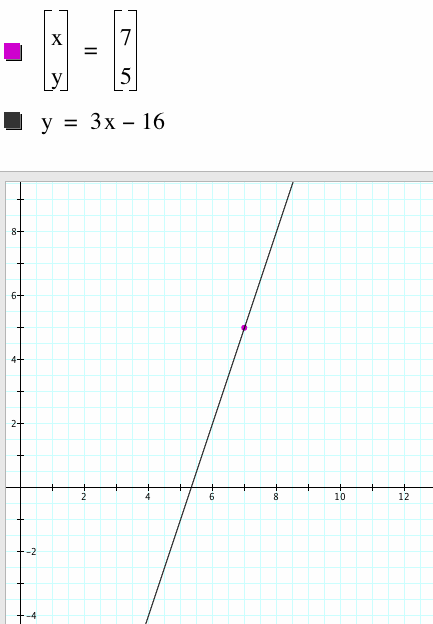
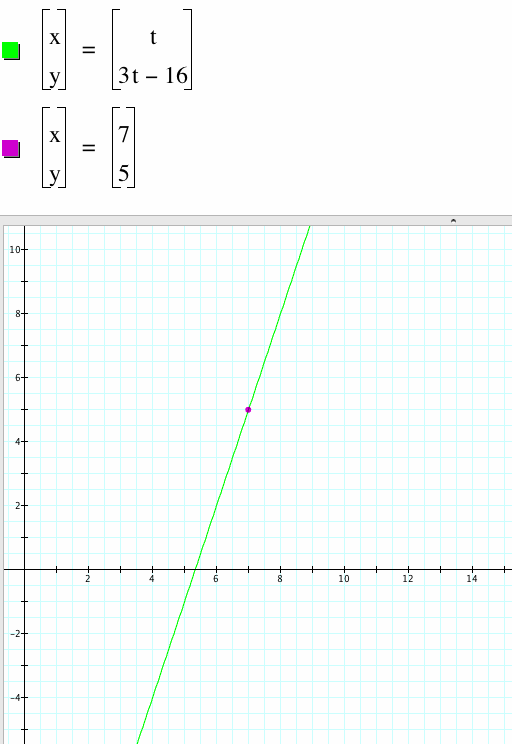
Step 2: Parameterize the line

Let x=t

Then y=3t-16

Let 0<t<10

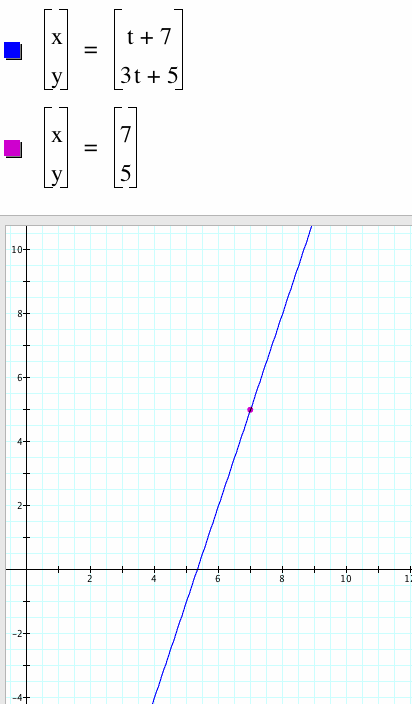
Alternative Parameterization

From the Point-Slope Form

y-5=3(x-7)

Let x=t+7

Then y=3t+5

Let -7<t<3

Check:

Solve for t

t=x-7

Plug into equation for y

y=3(x-7)+5

Generalization for any point and slope

Given a point (a,b) and a slope m

Point-Slope Form

y-b=m(x-a)

y=m(x-a)+b

Parameterization

Let x=t+a

y=mt+b

Check:

Solve for t

t=x-a

Plug into equation for y

y=m(x-a)+b

Return