Assignment 11:
Exploring
![]()
by
Margo Gonterman
Exploring Values of a, b, k
Case 1: Let a=b
Specifically, let a=2 and b=2.
Let's start by exploring integer values of k.

Note that when k=4 there are 4 "petals" on the flower. When k=2 there are 2 "petals".
In general, when k is an integer and a=b, the graph is called a "k-leaf rose"
What happens if k is not an integer?
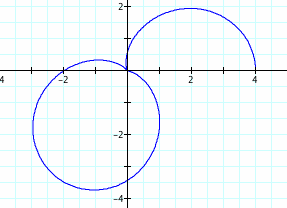
The initial graph looks like this. Note that the values of theta are![]() .
.
However, changing the values of theta to be ![]() yields the following graph.
yields the following graph.
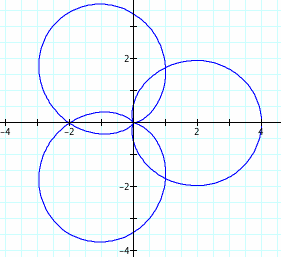
![]()
When k is a fraction m/n, notice that the flower has m petals, but the values of theta must be changed to![]() to view the entire graph.
to view the entire graph.
Below is an animation as k varies from -10 to 10. Notice that as k increases, the number of petals increase.
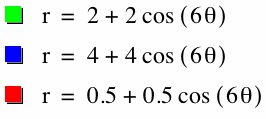

Notice that when a=b=2 and k=6, the graph is a 6 leaf rose with petals that have length 4.
What a=b=4, the graph is a 6 leaf rose with petals that have length 8.
What a=b=0.5, the graph is a 6 leaf rose with petals that have length 1.
Generally, when a=b, the length of the petals of the rose is 2a.
Below is an animation of a 6 leaf rose as a and b vary from -5 to 5. Note that the petals vary in size from 0 to 10.
Case 2: Let a<b
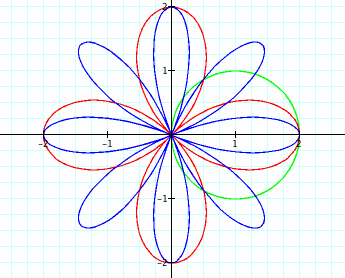
What if a=0?
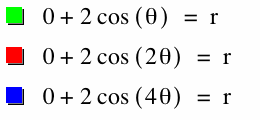 |
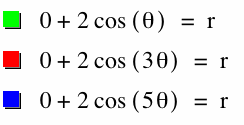 |
 |
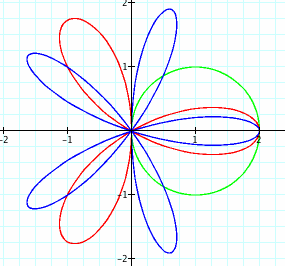 |
Notice that when a=0, the petals have length b.
Also, when k is even, there are 2k petals on the rose.
When k is odd, there are k petals on the rose.
Let's see if this holds when a≠0.
![]()
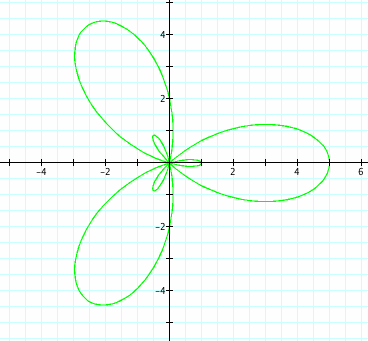
Notice that there are two sets of petals. There are 3 larger petals with length 5 and 3 smaller petals within the larger petals that have length 1.
Let's look at another example.
![]()

Here again, there are two sets of petals. There are 4 larger petals with length 5 and 4 smaller petals between the larger petals with length 3.
In general, when a<b, the flower will have two sets of petals.
The smaller set will have k petals of length b-a.
The larger set will have k petals of length b+a.
When k is even, the smaller petals lie between the larger petals.
When k is odd, the smaller petals line inside the larger petals.
Below is an animation of a flower with smaller petals of length 1 and larger petals of length 5 as the number of petals, k, varies.
![]()
Case 3: Let a>b
![]()
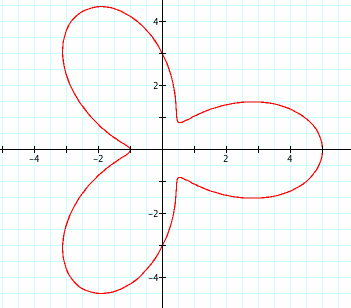
When a>b, the petals do not meet at the origin.
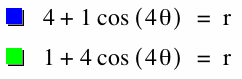
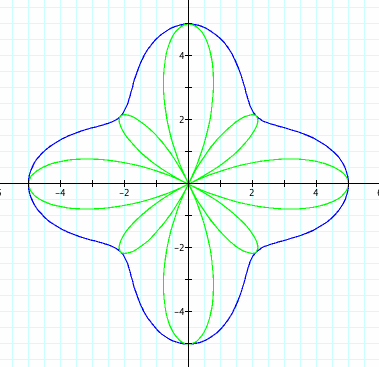
Notice the relationship between the two graphs above.
When a>b the largest part of the graph is still a+b and the smallest is a-b.
Below is an animation as k varies.
![]()
Below are a few more animations of the behavior of polar equations of the form
![]()
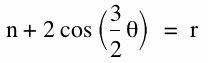 |
|
A Pretty Flower