Assignment 2:

Exploring

by

Margo Gonterman

The general form of a quadratic equation is:

The vertex form of a quadratic equation is:

The factored form of a quadratic equation is:

This investigation will focus on how the parameters a, b, and c in general form change the shape and orientation of the parabola.

What happens to the parabola as a varies?

• When a>0, the parabola opens up. When the parabola opens up, the vertex of the parabola is the minimum.
• When a<0, the parabola opens down. When the parabola opens down, the vertex of the parabola is the maximum.
• When a=0, the parabola degenerates into a line.
• As |a| increases, the parabola becomes more narrow.
• As |a| decreases, the parabola becomes wider.

See the animation below to watch what happens as a varies from -3 to 3.

What happens to the parabola as b varies?

As b varies from -3 to 3, note that the vertex of the parabola seems to trace along a parabola that opens down.

In fact, the vertex traces along the reflection of the original parabola when b=0.

The reflection of the parabola given by is .

Below is an animation of a parabola in standard form as b varies from -5 to 5 overlaid with its reflection when b=0.

What happens to the parabola as c varies?

• As c increases, the parabola shifts up vertically.
• As c decreases, the parabola shifts down vertically

Derivation of Quadratic Equation

From the general form of a quadratic equation, it is possible to derive the quadratic formula used to solve equations of this type.

1. Start with the general form of a quadratic equation 2. Subtract c from both sides 3. Factor an a out of both terms on the left hand side 4. Complete the square on the left hand side by adding (b/2a)^2 to both sides 5. Expand (b/2a)^2 and get a common denominator on the right hand side 6. Take the square root of both sides of the equation (Don't forget the +/- !!) 7. Simplify the denominator of the right hand side 8. Subtract b/2a from both sides

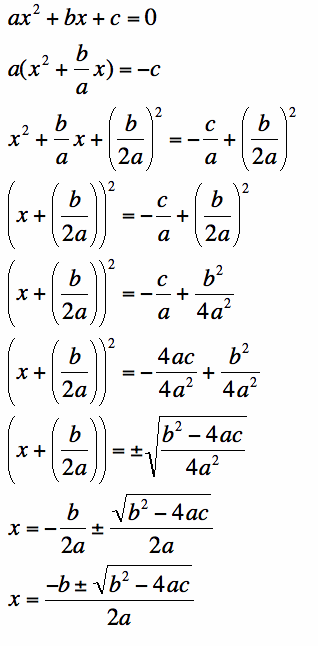Return