

![]()
Case 1. k=1
![]()
* When a=b, the shpe is not changed, but as number of a and b are getting bigger, the size is getting bigger.

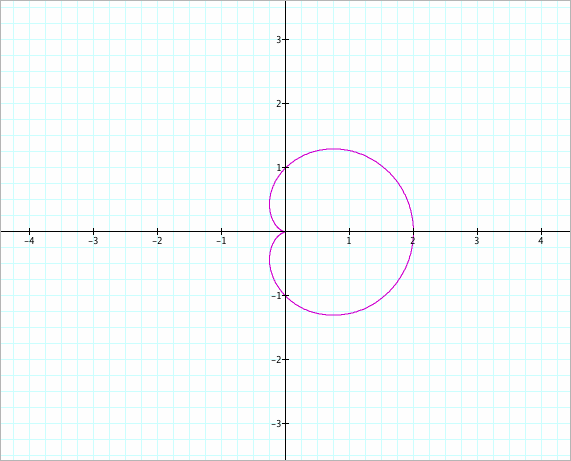
* When a<b, the shpe is changed. The shape like a circle emerges inside the original graph.
As the difference between a and b is getting bigger, inside circle is getting bigger.
![]()
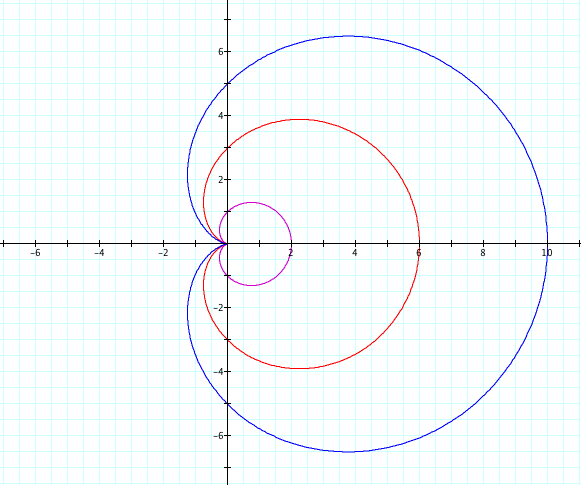
* When a>b, as a is getting bigger, the shape looks like a circle, and if a is bigger than b, the graph do not meet origin.
Case 2. k>1
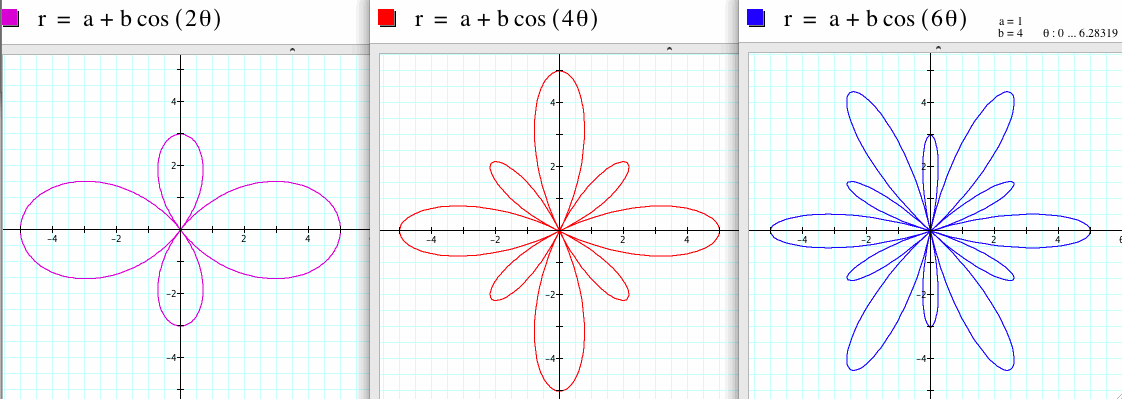
* When a=b, if k is an integer, and its number is getting bigger, then the shapes like a leaf are increasing.
If k=2, there are 2 leafs.
If k=3, there are 3 leafs.
According to NOTE in the page of Assignment 11, when a and b are equal, and k is an integer, this is one textbook version of the "n-leaf rose."
* When a<b, the shpe is changed. The shapes of leaf are added at the original graph, and these leafs are smaller than original leafs.
If k is even, the 2k leafs appear. If k=2, there are four leafs, that is, two are big, and the others are small. Big leafs alternate with small leafs.
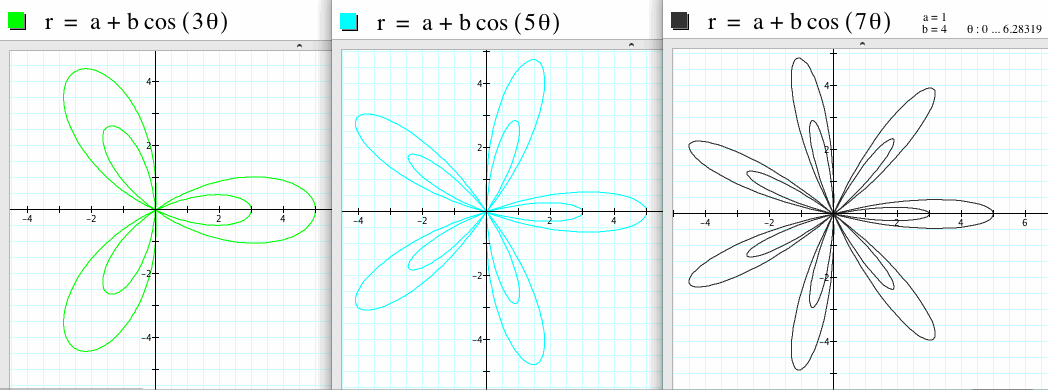
If k is odd, the 2k leafs appear. If k=3, there are six leafs, that is, three are big, and the others are small. However, small leafs are inside big leafs. They are overlaped.
In addition, if a is smaller than b very much, the small leafs are getting bigger.
* When a>b, the graph do not pass the origin.
If k is an integer, and its number is getting bigger, then the shapes which like a leaf are increased.
If k=2, there are 2 leafs.
If k=3, there are 3 leafs.
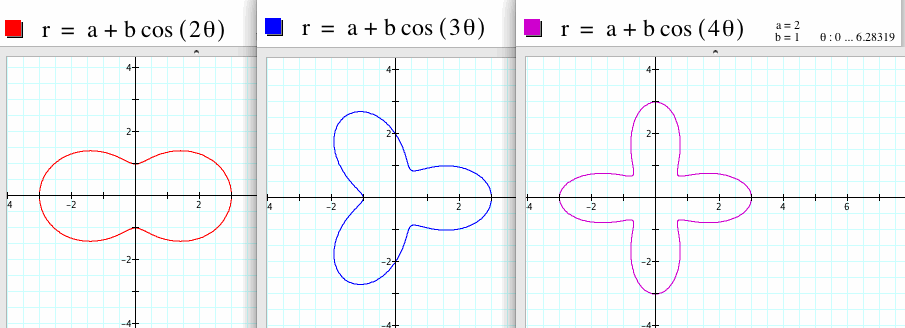
Moreover, if a is bigger than b very much, the shape becomes a circle.

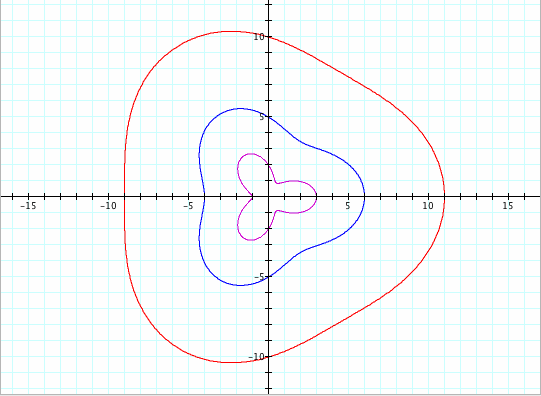
Compare with ![]() for various k.
for various k.
As b is getting bigger, the graph's size is getting bigger.
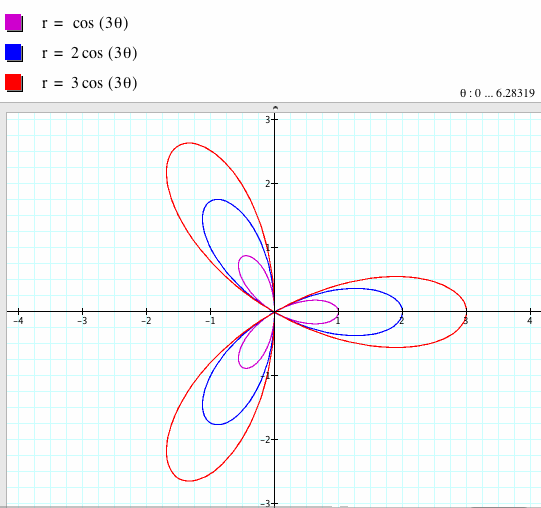
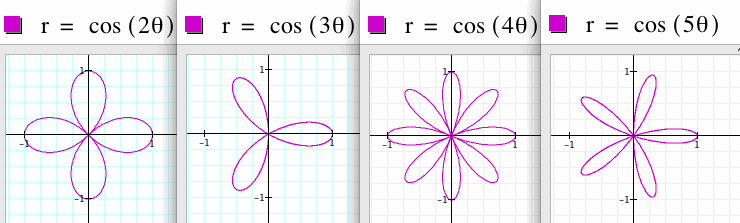
If k is increased, more leafs appear.
If k is even, 2k leafs appear.
If k is odd, k leafs appear.
What if .... cos() is replaced with sin()?
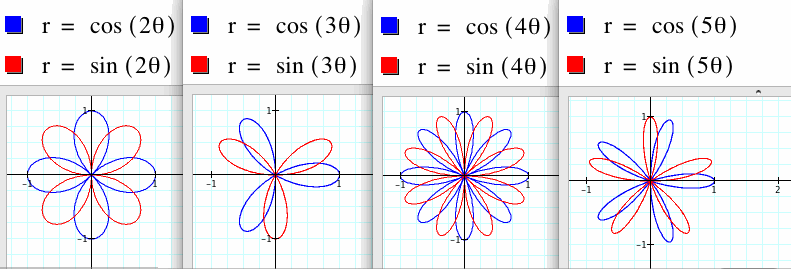
If cos() is replaced with sin(), the graph's slope is changed.