---

Day 2. The Properties of Matrices

Algebraic Properties of Matrix Operations

In this page, there are some general results about the three operations: addition(subtraction), multiplication, and scalar multiplication.

From now on, we will not write m-by-n but mxn.

<Properties involving Addition>

Let A, B, and C be mxn matrices. We have:

1. A+B = B+A (commutative property)

2. (A+B) + C = A + (B+C) (associative property)

3. A + O = A where O is the mxn zero-matrix (all its entries are equal to 0) (the identity of addtion)

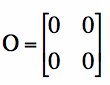
4. A+B = O if and only if B = -A. (the inverse of addition)

<Properties involving Multiplication>

1. Let A, B, and C be three matrices. If you can perform the products AB, (AB)C, BC, and A(BC), then we have:

(AB)C = A (BC). (associative property)

Note, for example, that if A is nxm, B is mxk, and C is kxl, then the above products are possible (in this case, (AB)C is nxl matrix).

2. If and are real numbers, and A is a matrix, then we have:

3. If is a real number, and A and B are two matrices such that the product is possible, then we have:

4. If A is an nxm matrix and O the mxk zero-matrix, then AO = O.

Note that AO is the nxk zero-matrix. So if n is different from m, the two zero-matrices are different.

5. In general, when the product AB and BA are possible. Thus, multiplication of matrix is not commutative.

<Properties involving Addition and Multiplication>

1. Let A, B, and C be three matrices. If you can perform the appropriate products, then we have:

(A+B)C = AC + BC

and

A(B+C) = AB + AC (distributive properties)

2. If and are real numbers, A and B are matrices, then we have:

and

There is a worksheet for multiplication.

CLICK HERE

<Identity and Inverse of Matrix>

- Identity Matrix

We have seen that matrix multiplication is different from normal multiplication (between real numbers). Are there some similarities? For example, is there a matrix which plays a similar role as the number 1?

(i.e., when is a real number, x1=1x=.)

The answer is yes. Indeed, there is a matrix which plays like the number 1 considering the nxn matrix.

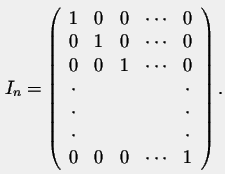
In particular, we have:

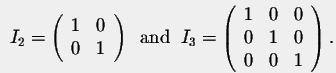
The matrix In has similar behavior as the number 1 in multiplication. For any nxn matrix A, we have:

The matrix In is called the Identity Matrix of order n (the identity of multiplication).

We can consider having the identity of multiplication as one of properities involving multiplication.

The identity matrix behaves like the number 1 not only among the matrices of the form nxn. Indeed, for any nxm matrix A, we have:

In particular, we have:

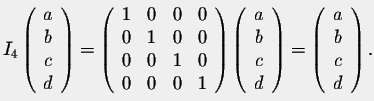
- Inverse Matrix

Definition. An nxn matrix A is called nonsingular or invertible iff there exists an nxn matrix B such that

where In is the identity matrix. The matrix B is called the Inverse matrix of A.

We can consider having the inverse of multiplication as one of properities involving multiplication.

Notatio: A common notation for the inverse of a matrix A is . So:

Let's find the inverse of

.

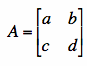Let

.

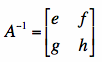Since , we get

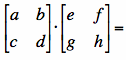
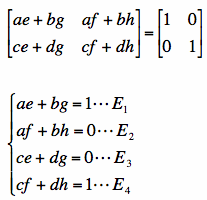
From E2, we can get:

.

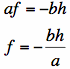Plug this into E4.

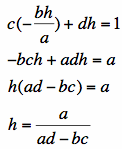
From E3, we can get:

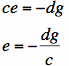
Plug this into E1.

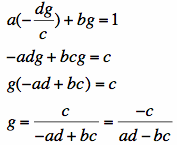
So, we can also find e and f by plugging g and h.

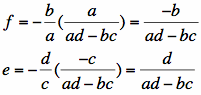
Thus, there is the inverse of A

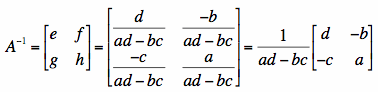
Therefore, we can present :

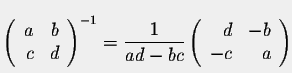
The inverse matrix is unique when it exists. So if A is invertible, then is also invertible and

The following basic property is very important: If A and B are invertible matrices, then AB is also invertible and

Since , we can know that .