Megan Langford

Let’s investigate the graph activity for functions involving

First, let us examine the graph of the equation

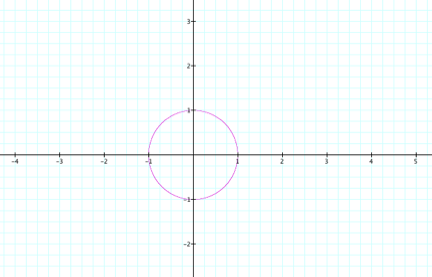
This is a commonly-known graph for the equation of a circle. It is completely centered at the origin, with a radius of 1.

Now, let’s examine the graph of the equation

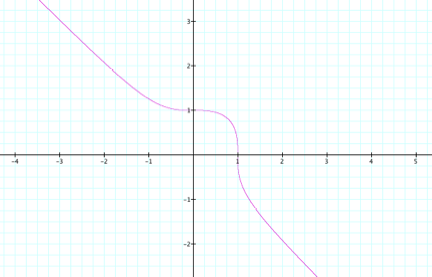
We can now notice that this graph has a similar shape to the last one in the first quadrant. However, from there, the lines simply extend out in the second and third quadrants to form almost a straight line.

Let’s go ahead and take a look at the graph for the equation

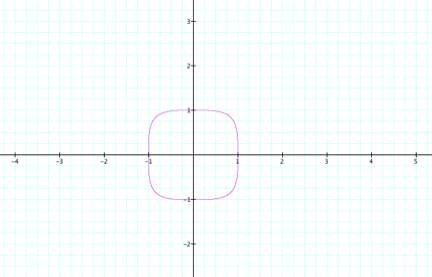
This graph is more similar to the first graph, and we can attribute this to the fact that both equations include even exponents. The main difference in this graph compared to the first one is that it has extended out to include four smooth corners, one in each quadrant.

Let’s compare another graph to these results. We will now take a look at the graph for the equation . Since this equation includes odd exponents, I am going to predict that its shape will be more similar to the graph.

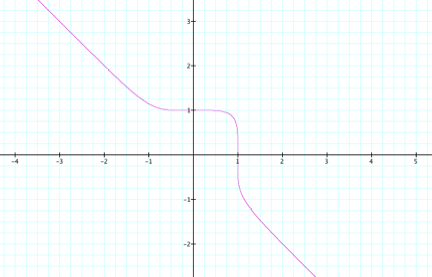
As predicted, this graph is much more similar to the graph of our second equation. The main difference is that the corners form a slightly steeper slope than they did in the previous graph.

To view these outcomes more easily, we will now show a graph including all four equations:

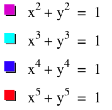
As we can see here, the four corners of the shape form a sharper curve as we increase the exponents.

To take this behavior to another level, let’s examine the graphs for and . I am going to predict that the graph with the even exponents will have almost a perfect square shape, and the graph with the odd exponents will form an elongated “W” shape along the same diagonal.

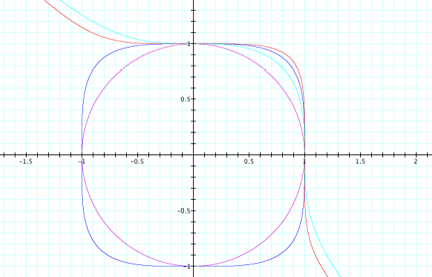
And now we graph

We can now see that our prediction was fairly accurate. If we were to continue to increase the function to any greater even integer value, then we would form sharper and sharper corners on the square figure of the graph.

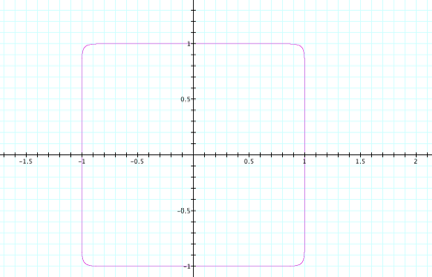
Now, let’s go ahead and look at the graph of

Again, our prediction of this graph was fairly accurate. If we were to continue to increase the exponents in the equation to any greater odd integer, we now know that the corners in the figure would continue to make a sharper shape.