Explorations with f(x)

Kasey Nored

Let f(x) = a sin(bx + c) and g(x) = a cos(bx + c).
Values were selected for a, b and c. a = 0.5; b = 1; c = 2

Our first graph is h(x) = f(x) + g(x)

It appears as a sine curve that has been shifted slightly.

Our second graph is h(x) = f(x)•g(x)

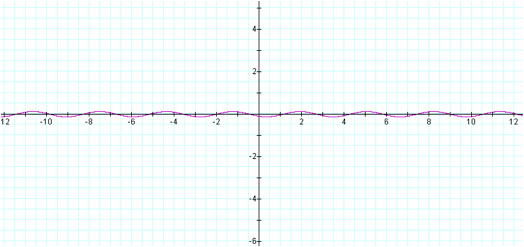
This curve is intentional represented with the same graph area to highlight the difference. The curve seems shifted and “squished” or flattened.

The third graph is .

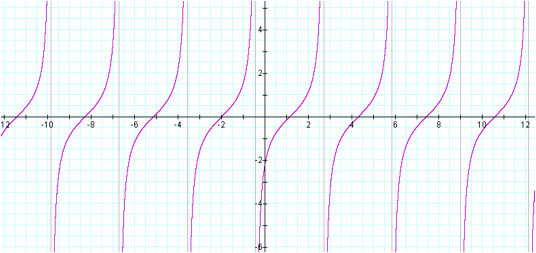
This provides a nice asymptote.

The fourth graph is h(x) = f(g(x)).

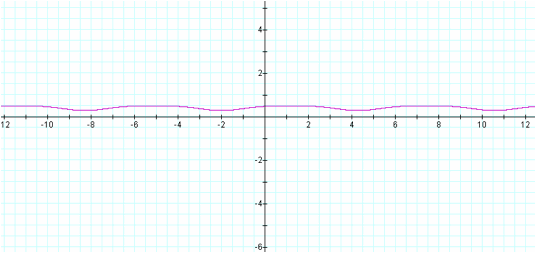
This curve is an interesting one and if you trace the function the curve has two maximums before it has an apparent minimum. However, this is an extremely close curve and representing it visually with the current software doesn’t make this clear.

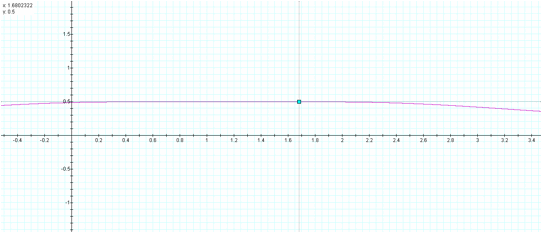
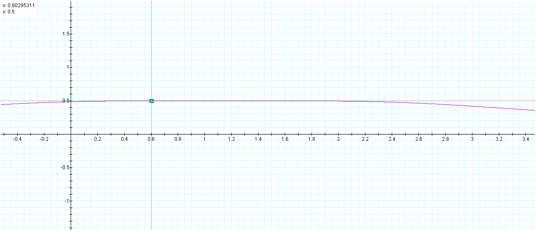
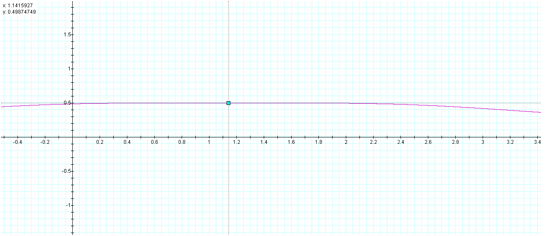
If you look very closely at the three preceding graphs you can see that y reaches 0.5 on both the positive and negative sides of the point (1.145927, 0.49874749).