Pedal Triangles

by Kasey Nored

A petal triangle is created by the picking of a point and constructing perpendicular lines between the point and the sides of a triangle which can be extended as necessary.

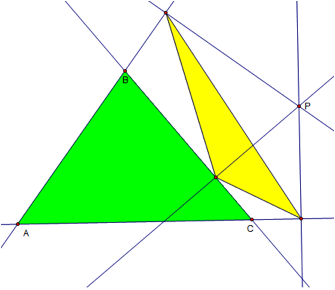
Our beginning triangle is ABC which is green and the pedal triangle is in yellow. Point P is our pedal point.

To further explore the pedal triangle we are looking at a pedal triangle of a pedal triangle of a pedal triangle where point P is the incenter of triangle ABC.

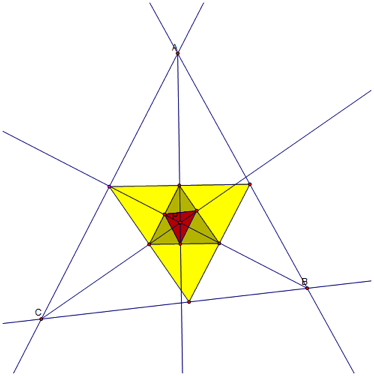
A few things jump out immediately such as the vertices of the second and third pedal triangle lie upon the angle bisectors of triangle ABC.

To explore the Simpson Line, the line where the vertices of the pedal triangle are collinear we need a circumcenter.

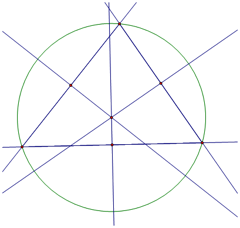
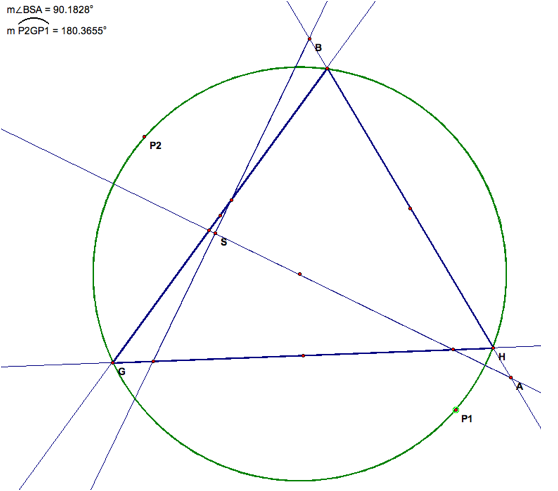
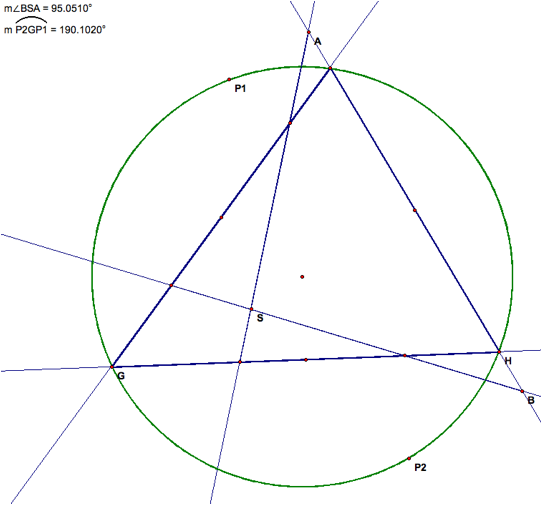
After hiding the perpendicular lines that provide us with a circumcenter, we created two Simpson lines, pedal triangles with point P on the circumcenter of the original triangle. The pedal points are labeled P1 and P2 and the intersection of the two lines upon which the pedal triangles lie is labeled S.

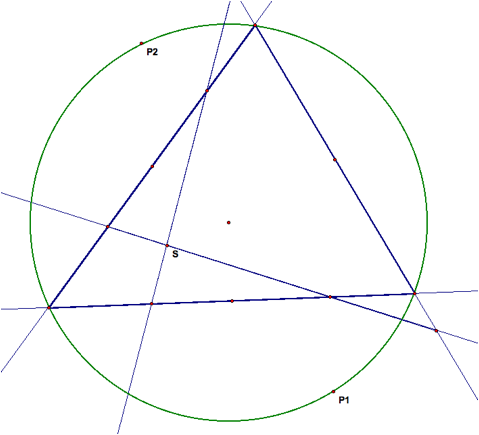
We want to explore the relationship between the arc measure between the two pedal points and the angle measure of the intersection of the Simpson lines.

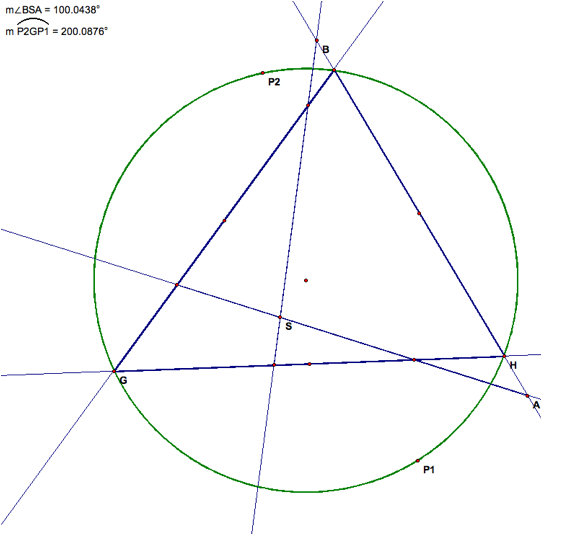
As you can see here the angle measure of the is equal to twice the measure of angle BSA, which is the opposite angle from the arc. This relationship is maintained regardless of the translation of the pedal points.