(1) Assume f(x) and g(x) are linear functions where : f(x) = 10x + 2

g(x) = 5x - 6

We will investigate the function above using the following equations:

(i) h(x) = f(x) + g(x)

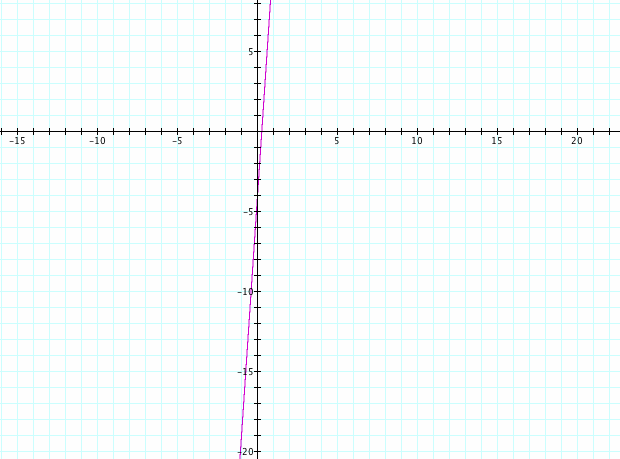
Graph of f(x) + g(x)

This graph illustrastes a straight line with an intersection at y-intercept (0, - 4)

(ii) h(x) = f(x) * g(x)

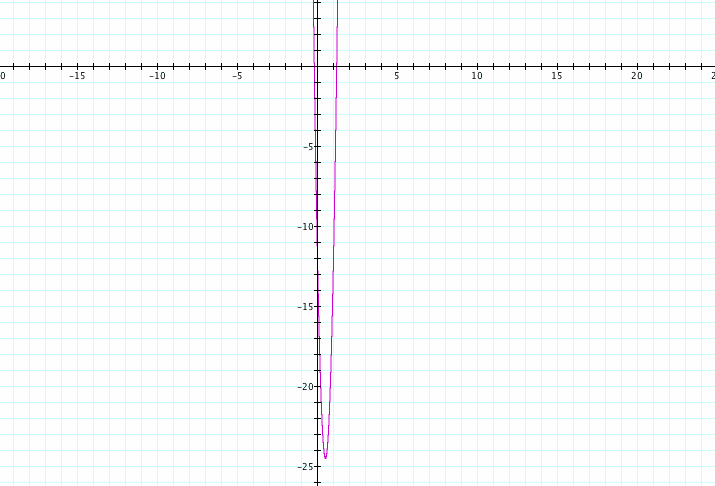
Graph of f(x) * g(x)

The product of two linear functions is a quadratic function. Therefore, the graph is going to be a parabola

(iii) h(x) = f(x) / g(x)

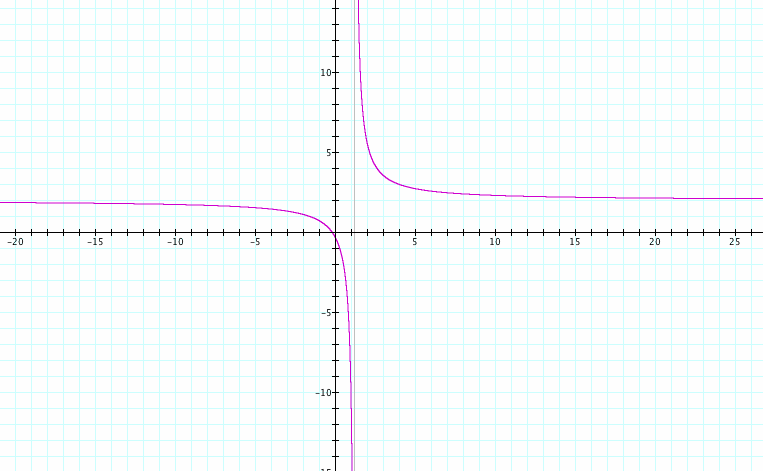
Graph of f(x) / g(x)

The division of two linear function produces an inverse function

(iv) h(x) = f(g(x))

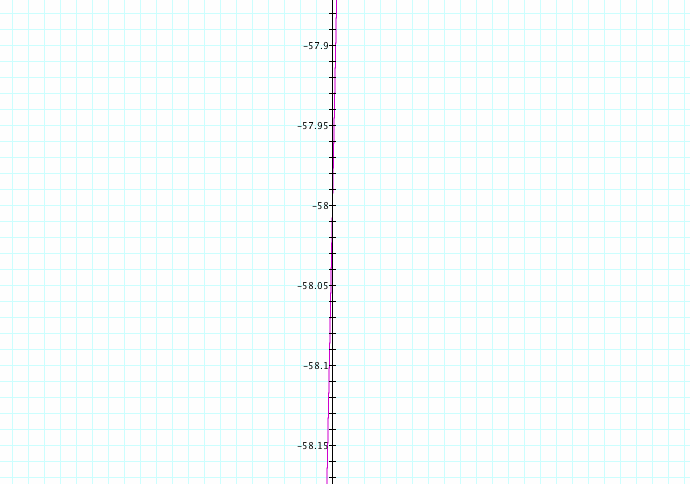
Graph of f(g(x))

The composition of two linear functions results in a single straight line with a y-intercept

(2) Assume f(x) and g(x) are linear functions where : f(x) = 10x - 5

g(x) = 3x - 2

We will investigate the function above using the following equations:

(i) h(x) = f(x) + g(x)

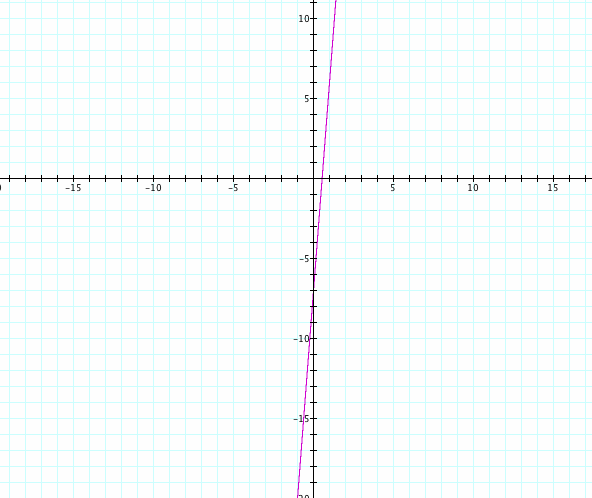
Graph of f(x) + g(x)

This graph illustrastes a straight line with an intersection a y-intercept (0, - 4)

(ii) h(x) = f(x) * g(x)

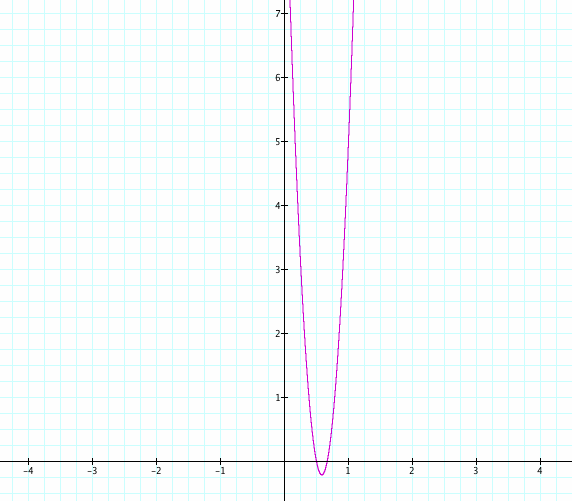
Graph of f(x) * g(x)

The product of two linear functions is a quadratic function. Therefore, the graph is going to be a parabola as shown in the graph above

(iii) h(x) = f(x) / g(x)

Graph of f(x) / g(x)

The division of two linear function produces an inverse function

(iv) h(x) = f(g(x))

Graph of f(g(x))

The composition of two linear functions as stated previously, results in a single straight line with a y-intercept (0, - 25)

Conclusion

From the above examples, we see the patterns that occur when graphing linear functions. The algebraic proofs are shown.

- The addition or composition of two linear functions would result in a straight line graph.

Proof:

Given two linear functions f(x) = ax + b and g(x) = cx + d.

Then f(x) + g(x) = ax +b + cx + d = (a+c)x + (b+d). Thus, it results in a linear function with a slope a+c and y-intercept at b+d

- The multiplication of two linear functions, is going to become a quadratic function and the graph would be a parabola.

Proof:

Given two linear functions f(x) = ax + b and g(x) = cx + d.

Then f(x) * g(x) = (ax +b) (cx + d) = acx^2 + adx + bcx + bd = acx^2 + (ad+bc)x + bd. Thus, it results in a quadratic equation.

- The composition of two linear functions as stated previously, results in a single straight line

Proof:

Given two linear functions f(x) = ax + b and g(x) = cx + d.

Then f(g(x)) = a(cx+d) + b = acx + ad + b which is a linear function with slope ac.

g(f(x)) = c(ax+b) + d = acx + bc + b which also has slope ac meaning f(g(x)) and g(f(x)) are parallel.

Return to homepage