

Exploring Tangent Circles
by
Molade Osibodu
Objective: To show the construction of tangent circle and some properties associated with it
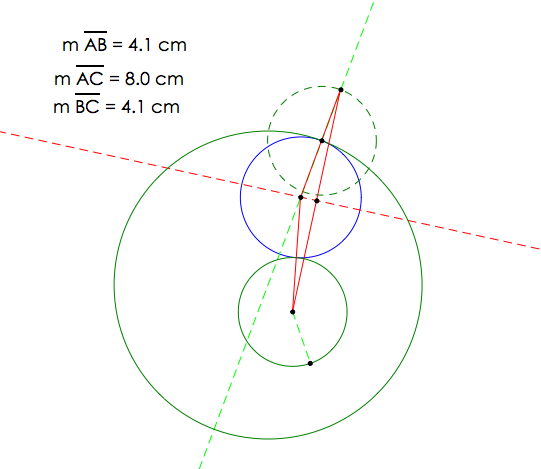
Case 1: Construct a big circle and a smaller circle inside the big circle. Then choose an arbitrary point on the big circle and construct a line from the arbitrary point to the center of the circle.
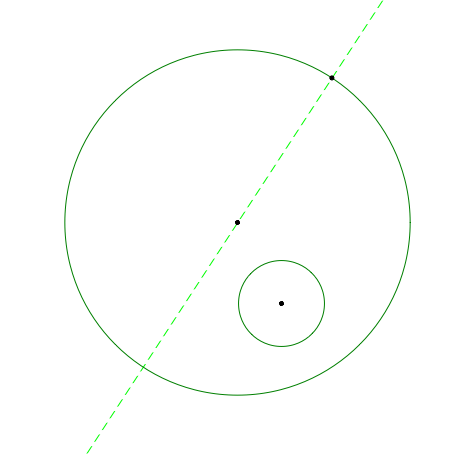
Next, construct a circle around the arbitrary point by using the radius of the small circle.
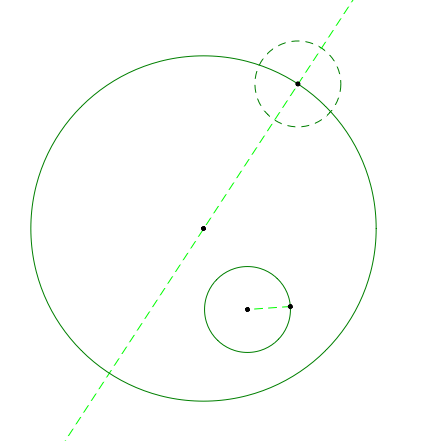
Now create a segment from the intersection point of the new circle with the line to the center of the small circle. Construct the midpoint of the new line and then construct a perpendicular line from the midpoint to the line
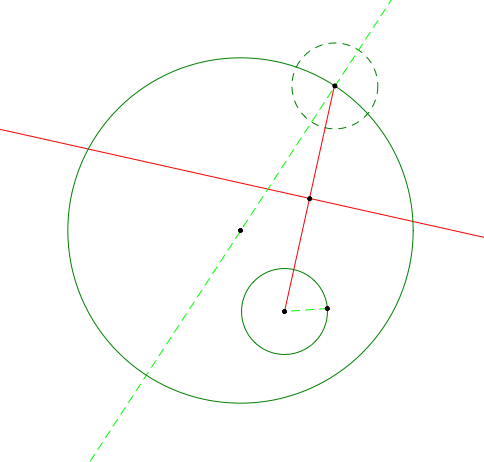
Create a circle from the intersection point of the perpendicular line and the green line and from the intersection of the big circle and green line to construct the tangent circle
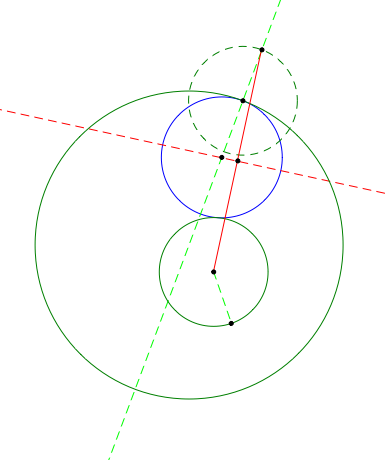
Note that the triangle formed from connecting the segments as shown below is an isosceles triangle.
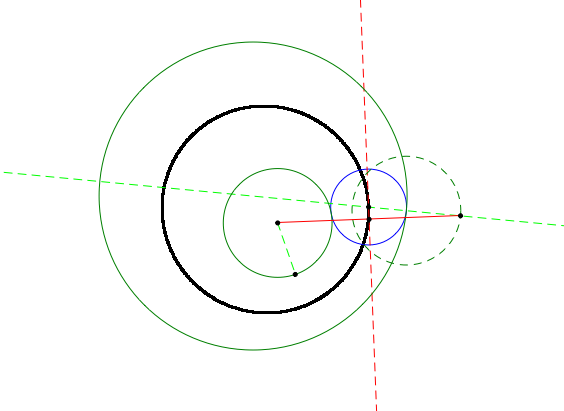
The tangent circle is shown in black in the figure shown below.
Case 2: Construct two circles of the same size. Then choose an arbitrary point on the either of the circles and construct a line from the arbitrary point to the center of the circle.
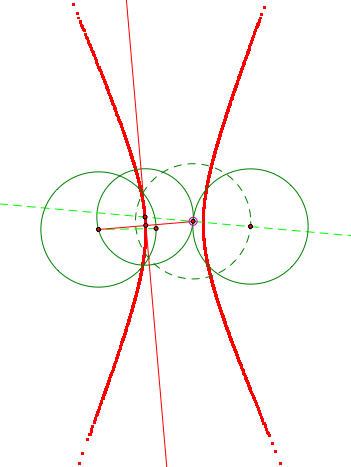
We see that an hyperbola is formed and the hyperbola is equal distance from both of the circles.