Pedal (Faster!) Triangles

by

Mike Rosonet

This page will look at the relationship of a pedal triangle with the original triangle.

Here is a GSP script tool of a pedal triangle. Drag the point P around to view different pedal triangles for the different locations of pedal point P.

Below are two examples of pedal triangles, one with an interior pedal point and the other with the exterior pedal point.

One pedal triangle, given a pedal point P inside the given triangle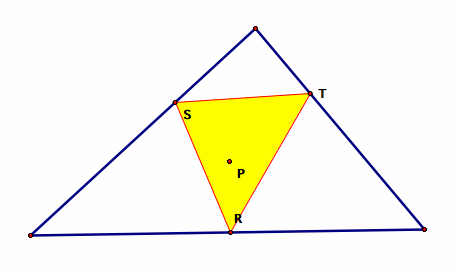

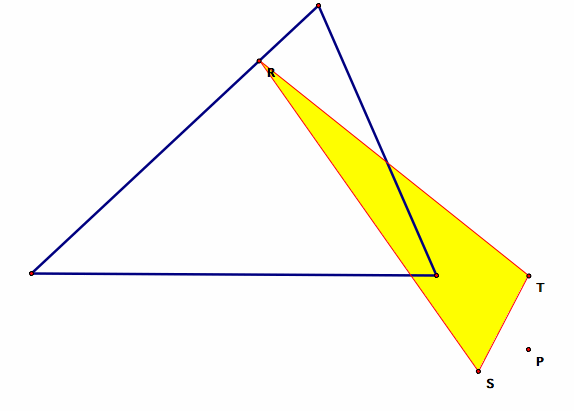One pedal triangle, with exterior pedal point P

 

There is an observation to be made about interior pedal points. As the pedal point is moved around the interior of the triangle, it appears that the pedal triangle remains in the interior of the given triangle as well.

Extension 1

Can this be proven? That is, if a pedal point is in the interior of a given triangle, will the pedal triangle be constructed in the interor of the given triangle as well?

Extension 2

This same observation obviously cannot be made about exterior pedal points. However, the pedal triangles of exterior pedal points can be totally inside of the given triangle, can be intersecting at least one side of the given triangle, and can be completely outside of the given triangle. One proof worth looking at is determining where an exterior pedal point must be in order to construct a pedal triangle that is completely inside the given triangle, where the exterior pedal point must be placed in order to construct a pedal triangle that intersects at least one side of the given triangle, and where the exterior pedal point must be placed in order to construct a pedal triangle that is completely outside of the given triangle.

Find where a pedal point must be located exterior of the given triangle so that the pedal triangle will be constructed

What if the pedal point is the centroid of the triangle?

To investigate this question, it is necessary to find the Centroid of the triangle. To do so, construct the triangle's medians by locating the midpoints of the sides of the triangle and constructing segments from the vertices to the midpoints opposite them. The medians are concurrent, and the point of concurrency is the Centroid of the triangle.

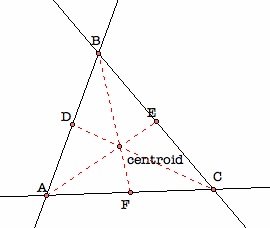
the centroid of triangle ABC

In this figure, the midpoints of the sides of triangle ABC are the points D, E, F. Medians have been constructed from each vertex to the midpoint opposite, locating the Centroid of triangle ABC.

Now, let the Centroid be the pedal point. Construct the pedal triangle of the Centroid by constructing altitudes from the Centroid to each side of the triangle. Construct segments between the feet of the three altitudes. The triangle constructed between the feet of the altitudes is the pedal triangle.

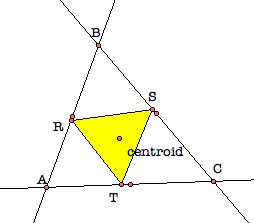
the pedal triangle of the centroid

In this figure, the feet of the altitudes are the points R, S, T. By constructing segments between the feet of the altitudes, the pedal triangle is formed.

Thus, the pedal triangle will always be contained within the given triangle if the pedal point is the centroid of the given triangle.

What if the pedal point is the incenter of the triangle?

To investigate this question, construct the incenter of the triangle by constructing the angle bisectors of the angles of the triangle; the point of concurrency is the incenter of the triangle.

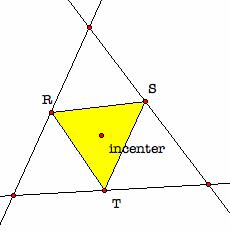
the pedal point P located at the incenter

The incenter is the center of the incircle, which is an inscribed circle that is tangent to the sides of the triangle at the feet of the altitudes constructed from the point of concurrency of the angle bisectors to the sides of the triangle. Recall that any point of tangency on a circle is a the point where the tangent line is perpendicular to the radius of the circle through that particular point on the circle.

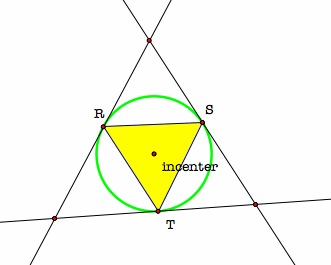
the incircle through the vertices of the pedal triangle

Thus, the feet of the altitudes of the incenter and the vertices of the pedal triangle are the same points. Click and drag any vertex of the triangle in this GSP file. Notice that the relationship between the feet of the altitudes constructed from the incenter and the vertices of the pedal triangle holds regardless of where the vertices of the original triangle are dragged to.

There are conditions in which the position of the pedal point will create a degenerate triangle, meaning that the three vertices of the triangle are all colinear. When this occurs, the line on which the three vertices lie is called the Simson line.

One instance in which this occurs is when the pedal point is located at one of the triangles vertices.

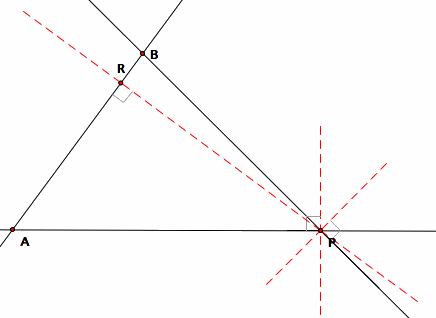
the pedal point P is located at vertex C

Let the red dashed lines represent the altitudes. Since the pedal point is located at a vertex, the altitudes constructed from the pedal point to the two sides of angle BPA each meet at the pedal point, as shown above. The only altitude whose foot is not the pedal point is the altitude to side AB, which is the remaining side of the triangle. Thus, a pedal triangle of a pedal point located at one of the vertices of the triangle will be degenerate, with only one of its sides visible. This altitude (in the figure above, segment PR) is the Simson line.

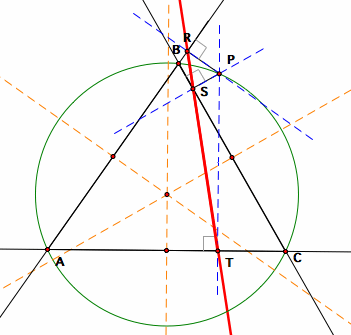
One other instance in which the pedal triangle is degenerate, forming another Simson line, is when the pedal point is located on the circumcircle of the triangle. In order to show this, it is necessary to construct the circumcenter of the triangle.

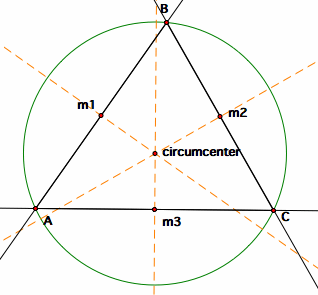
the circumcenter and circumcircle of triangle ABC

To construct the triangle's circumcenter, construct the midpoints of the sides of the triangle. Then, construct lines perpendicular to the sides of the triangle through each midpoint. The point of concurrency of the perpendicular bisectors of the triangle is the circumcenter. The circumcircle is the circle constructed through each of the vertices of the triangle with the circumcenter as its center.

Now, place the pedal point on the circumcircle and construct altitudes to the sides of the triangle. Then, draw lines between the feet of the altitudes.

the line connecting the feet of the altitudes when the pedal point P is located on the circumcircle of the triangle

Let the blue dashed lines be the altitudes constructed from the pedal point P and points R, S, T be the feet of the altitudes. By constructing lines between the feet, it is clear that the feet of the altitude are colinear. In fact, this is the case when the pedal point P is located anywhere on the circumcircle of the triangle.

By tracing the image of the Simson line as the pedal point P is moved along the circumcircle, the envelope of the Simson line creates a particular geometric shape.

the envelope of the Simson line as the pedal point moves along the circumcircle

The envelope of the Simson line as the pedal point P moves along the circumcircle is a deltoid. Here's a GSP file to see the animation of the Simson line, if necessary.

Return