Linear Explorations

By: Brandie Thrasher

What are linear equations? As defined by dictionary.com, it is an equation in which the highest degree is the first power. An example of a linear equation would be:

y = x + 4

Let’s take a look at its graph

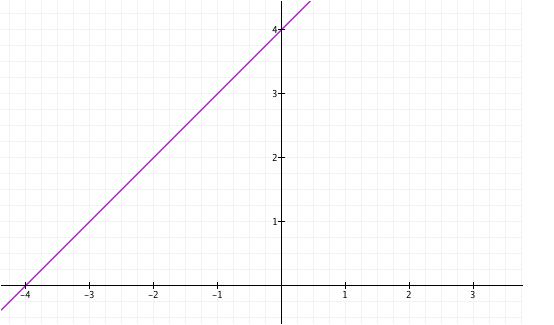
Let’s take a look at the graph that contains the following linear equations:

y = x + 4

y = x + 3

y = x + 2

y = x + 1

y = x + 0

y = x + (-1)

y = x + (-2)

y = x + (-3)

y = x + (-4)

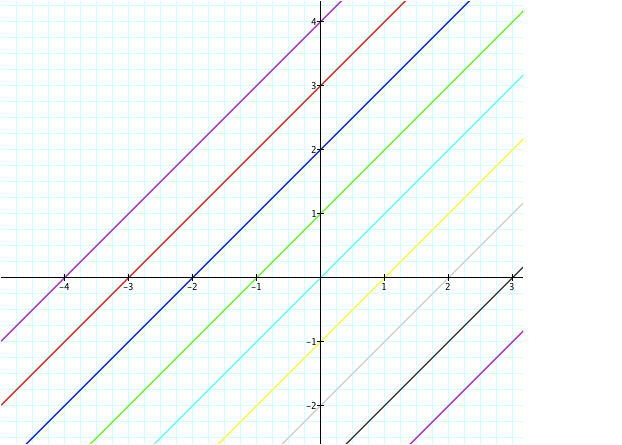
It appears that the graphs seem to be somewhat similar. Considering that they are all in the form of y = mx +b, each equation shares the same slope (m value) in which each line will “rise and run” the quantity of m. For these equations, our m value is 1.

These lines also carry another property in regards to sharing the same slope, they will NEVER intersect, and thus they are deemed as being parallel to one another.

Also, b is used to express the point at which the graph will intersect the y-axis. In each case shown, our graphs intersect the y-axis at each number representing b.

These conjectures will always hold true for y = x + n.

See ANIMATION

Return