Mathematics Problem Presentation
for EMAT 7050 Fall 2009 (Dr. A. Conner)
-- Which ball to shoot?
Chen Tian
ctianxa@uga.edu
In Sep. was the Snooker Shanghai
Masters 2009 held. I got the news that Ronnie O'Sullivan, nicknamed "the
Rocket" due to his rapid playing style, an English professional snooker
player, booked his place in the semi-finals of the Shanghai Masters with a 5-3
win over Ding Junhui, a talented Chinese snooker
player. O'Sullivan said: "Ding was first in the balls in every frame.
He'll be disappointed because he might feel he deserved to win." Anyway,
this gave me the inspiration to make up a problem like the following one.
One of the rules of snooker is to
hit one color ball between two red balls. Now O'Sullivan needs to use the cue
ball to shoot a color ball after a red ball. By the way, color balls worth more
points (Black 7; Pink 6; Blue 5; Brown 4; Green 3; Yellow 2), so he would be
glad to do that.
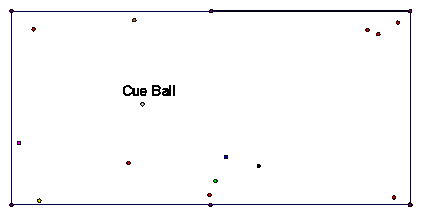
1) In the situation shown in the above figure, is it highly possible to pot
a color ball without hitting any cushion?
2) If not, then, O¡¯Sullivan tries to hit the center of the front surface of
the cue ball to push one color ball to hit the rubber cushions once or more to
go into one of the pockets. But it¡¯s hard to make a 2-or-3-cushion shot in
snooker. I want to see a fancy shot so I will let O¡¯Sullivan play on an
ordinary table, which has larger pockets. And we ignore the friction, air
resistance, etc. Now, in your opinions, which one has the highest possibility
to be potted in? How would you estimate it? What will the route of your object
ball be? Note the name ¡°cue ball¡± does help you start.
3)
Can you explain why these
two angles (of incidence & of reflection) are equal? Do you need a
protractor to construct the angles?
4)
Of course, you can use
straight edge and compass. Essentially, in order to ¡°estimate¡± the route of the
object ball, you can use a marked ruler, and estimate by just looking whether a
line is perpendicular to another line. (Why?)
5) If we suggest O¡¯Sullivan choosing the blue ball, do you have any other
way to check your suggestion? What is it?
6)
Have you noticed two
parallel lines? Why?
You may want to check out the GSP
script tools I created for this problem:
http://jwilson.coe.uga.edu/EMAT6680Fa09/Tian/Assignment%205/Chen%20Scripts.html
By the way, in billiards sports
professional players use their rich experience and fantastic skills and
sometimes the ¡°diamond system¡± (though not as precise as you may think; just a reference
object) on the table to help them square the direction of their cue.
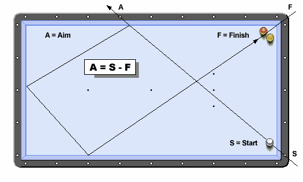
Figure cited from
http://www3.sympatico.ca/eric.perreault/diamond_system_en.html
The main mathematical knowledge involved
in the problem of finding the route of object ball:
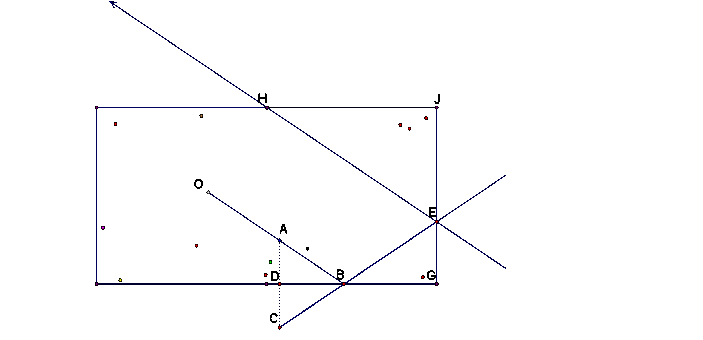
If we hit the center of the front
surface of the ¡°cue¡± ball, namely, O here, then O, A, B are
¡°collinear¡±. Both physically and mathematically if we ignore the friction, air
resistance, etc., then the angle of incidence equals the angle of reflection
(force decomposition), in symbols, ![]() and
and ![]() . How can we construct these angles? We construct AC
perpendicular to BD at D such that AD=CD. Draw ray CB meeting GE at E;
similarly, construct BF perpendicular to GE at E such that BG=FG. Draw ray FE
theoretically passing through point H, as desired. By
construction
. How can we construct these angles? We construct AC
perpendicular to BD at D such that AD=CD. Draw ray CB meeting GE at E;
similarly, construct BF perpendicular to GE at E such that BG=FG. Draw ray FE
theoretically passing through point H, as desired. By
construction ![]() , so
, so ![]() . But
. But ![]() ¡¡since they are
vertical angles. So we have
¡¡since they are
vertical angles. So we have ![]() ¡¡by transitivity of
angle equality. Similarly,
¡¡by transitivity of
angle equality. Similarly, ![]() . The mathematical idea of this construction also
works for some other problems like ¡°the shortest distance problem¡± or ¡°the
image of mirror problem¡±.
. The mathematical idea of this construction also
works for some other problems like ¡°the shortest distance problem¡± or ¡°the
image of mirror problem¡±.
To prove line OB is parallel to
line HE (in Euclidean geometry):
We have several theorems in
Euclidean geometry to prove two lines are parallel. We can choose to prove the two
corresponding angles along the transversal are equal or to prove the sum of the
two interior angles on the same side of the transversal equals 180 degrees. Both
of them use essentially the same mathematical reasoning. I will show the proof
using the latter parallel principle as follows.
![]() ¡¡since
the sum of interior angles of any triangle is
¡¡since
the sum of interior angles of any triangle is ![]() and
and ![]() ¡¡is this problem is
the corner of the pool table which can be abstracted as a right angle.
¡¡is this problem is
the corner of the pool table which can be abstracted as a right angle.
![]() ¡¡since
¡¡since
![]() ,
, ![]() ,
, ![]() ¡¡all together compose
a straight angle DBG, and
¡¡all together compose
a straight angle DBG, and ![]() as shown above, and similarly,
as shown above, and similarly, ![]() .
.
Thus, ![]() .
.
By distributivity,
![]() .
.
So ![]() .
.
Hence, ![]() , as desired.
, as desired.
Where the problem fits in Georgia
Performance Standards
GEOMETRY
v M6G1. Students will further develop their understanding of plane
figures.
v a. Determine and use lines of symmetry.
v M7G1. Students will construct plane figures that meet given conditions.
v a. Perform basic constructions using both compass and straight edge,
and¡¡¡¡¡¡¡¡ appropriate technology.
Constructions should include copying a segment; copying an angle; bisecting a
segment; bisecting an angle; constructing perpendicular lines, including the
perpendicular bisector of a line segment; and constructing a line parallel to a
given line through a point not on the line.
v b. Recognize that many constructions are based on the creation of
congruent triangles.
v M8G1. Students will understand and apply the properties of parallel and
perpendicular lines and understand the meaning of congruence.
v a. Investigate characteristics of parallel and perpendicular lines
both algebraically and geometrically.
v b. Apply properties of angle pairs formed by parallel lines cut by a transversal.
v d. Understand the meaning of congruence: that all corresponding
angles are congruent and all corresponding sides are congruent.
Process Standards
M8P1. Students will solve
problems (using appropriate technology).
b. Solve problems that arise
in mathematics and in other contexts.
c. Apply and adapt
a variety of appropriate strategies to solve problems.
M8P2. Students will reason and
evaluate mathematical arguments.
a. Recognize reasoning and proof
as fundamental aspects of mathematics.
b. Make and investigate
mathematical conjectures.
d. Select and use various
types of reasoning and methods of proof.
M8P3. Students will communicate
mathematically.
M8P4. Students will make
connections among mathematical ideas and to other disciplines.
a. Recognize and use connections
among mathematical ideas.
b. Understand how mathematical
ideas interconnect and build on one another to produce a coherent whole.
c. Recognize and apply
mathematics in contexts outside of mathematics.
M8P5. Students will represent
mathematics in multiple ways.
a. Create and use representations
to organize, record, and communicate mathematical ideas.
c. Use representations to
model and interpret physical, social, and mathematical phenomena.