Chen Tian

For EMAT6680 Fall 2009

There are a few ways to prove the concurrency of the three medians of any triangle.

(1)Brief proof.

Using Ceva's theorem: In a triangle ABC, three lines AM, BD and CE intersect at a single point G if and only if

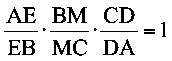
We will see that AE=EB, BM=MC, CD=DA, so . Therefore, the three medians intersect at only one point G.

(2)Brief proof.

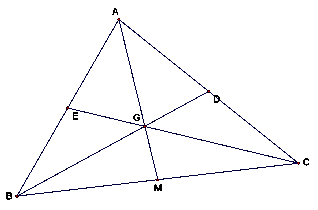
Given any triangle ABC, then D, E, M are, respectively, midpoints of AB, AC, BC. Join DE, DM.

Thus, we can prove ED||BC and EBMD is a parallelogram. So ED=BM=MC=(1/2)BC. And then by similarity we know that ED:BC=EG:GC=DG:GB=1:2. In other words, G can be described as the point on the median BD which is 2/3 of the way from B to D. Reversing the roles of A and C would therefore show that the third median AM also passing through G. Thus, all three medians meet in the point G.

Note: we, by the way, get a special property of the centroid of a triangle that the centroid G lies on each median 2/3 of the way from the vertex to the midpoint of the opposite side.

If you want you can use the calculation function of GSP to check this property.

(3)Brief proof in Vector Space.

We put vertex C on the origin, thus we consider OA, OB as vectors.

Join BD, OF, which intersect at G.

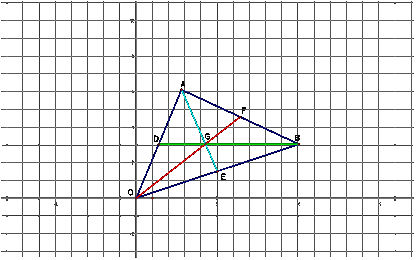
Based on (2) we know the centroid G lies on each median 2/3 of the way from the vertex to the midpoint of the opposite side.

Thus, AB=OB-OA, and AF=(1/2)AB.

So, OF=OA+AF=OA+(1/2)(OB-OA)=(1/2)(OB+OA).

Then try OG=(2/3)OF=(1/3)(OB+OA).

Similarly, BD = OD-OB = (1/2)OA- OB.

Then try BG’=(2/3)BD=(1/3)OA-(2/3)OB (where G’ is on BD 2/3 of the way from B to D).

And so OG=OB+BG’=(1/3)(OA+OB).

Therefore, G and G’ coincide.

Now we switch the roles of A and B, and then we can similarly show AG’’ coincides with AG (where G’’ is on AE 2/3 of the way from A to E).

So we conclude that the three medians insect at the same point G.

Return to my homepage for EMAT6680