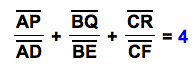Orthocenter & Altitude

by

Jane Yun

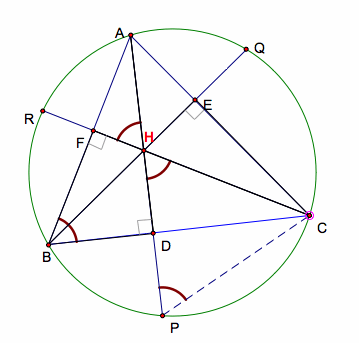
In this exploration, we will construct any inscribed acute triangle, ∆ABC, in the circle, draw three altitudes AD, BE, and CF, and extend AD, BE, and CF toward P, Q, & R so that it will intersect the circle. Then, we want to find

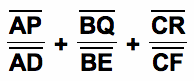
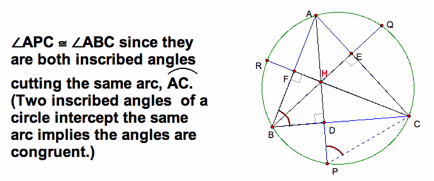
First, we are going to prove that HD = DP, HE = EQ, and HF = FR.

Proof: Let ∆ABC be any acute triangle that is inscribed in the circle and let AD, BE, and CF be the altitudes.

Extend AD, BE, and CF toward P, Q, & R so that it intersects the circle.

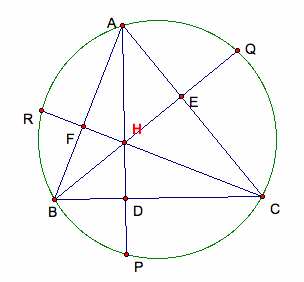
Want to prove that HD = DP.

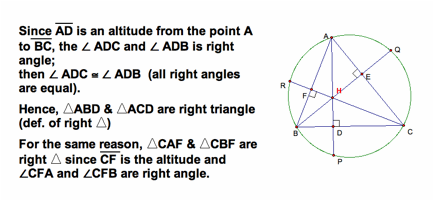
Join CP

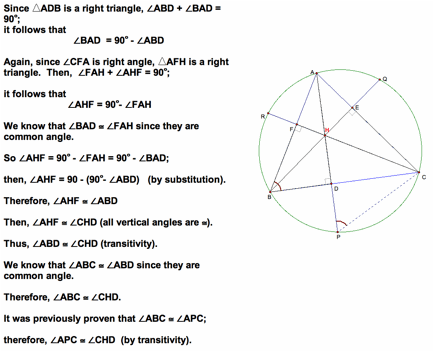
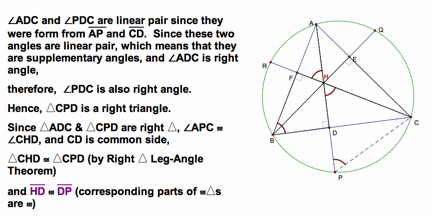
Therefore, HD = DP.

Similarly, we can prove that the HE = EQ and HF = FR.

Q.E.D

Now, we want to find

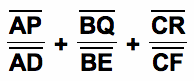
By looking at the construction,

AP = AD + DP

BQ = BE + EQ

CR = CF + FR

Then, by substitution

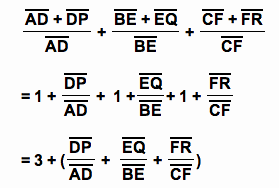
Since HD = DP, HE = EQ, and HF = FR,

this is equivalent to

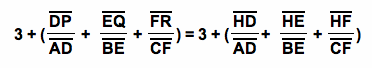
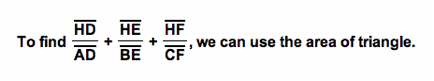
Area of ∆BHC + Area of ∆CHA + Area of ∆ABH = Area of ∆ABC.

Area of ∆BHC = ½ (HD * BC)

Area of ∆CHA = ½ (BE * CA)

Area of ∆ABH = ½ (CF * AB)

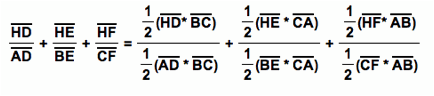
Since area of ∆ABC = ½ (AD * BC) = ½ (BE * CA) = ½ (CF * AB), area of ∆BHC = ½ (HD * BC),Area of ∆CHA = ½ (BE * CA), and area of ∆ABH = ½ (CF * AB),

then

Therefore,

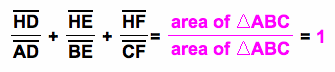
Now, previously shown that

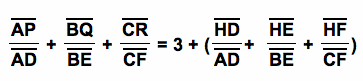
and since

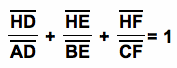
therefore,

Therefore,

---

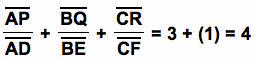
Return to Jane's Homepage

---