---

William Plummer - Assignment #1

Examine the following formula:

and its graph:

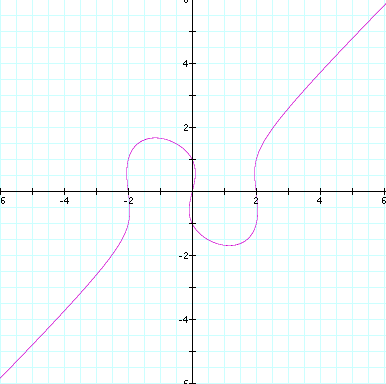
When the 4 in the equation is replaced by other numbers, the shape of the graph changes

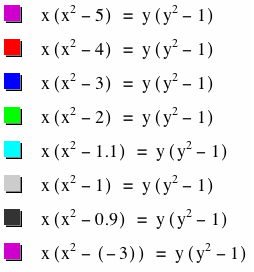
The above substitutions for 4 resulted in the following graphs:

As n changes, the graph consistently intersects the y axix at 1, 0, and -1

In the graph below, press the play button to see how the graph changes as n changes.

As n increases, the curve in the second and fourth quadrants expand and the graph intersects the x axis at:

As n decreases, the curve in the second and fourth quadrants shrink until n equals the subtrahend in the second set of parenthesis.

In this case the subtrahend is 1.

As n continues to decrease past the second subtrahend, the graph changes again into an “S” shape that continually becomes thinner, still intersecting the y-axis at 1, 0, and -1.

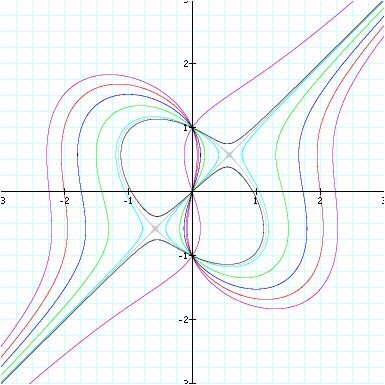
When both subtrahends are equal to some number n, the graph takes on the shape of an ellipse bisected by the line y = x.

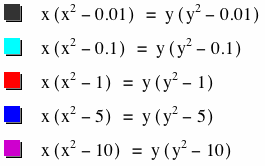
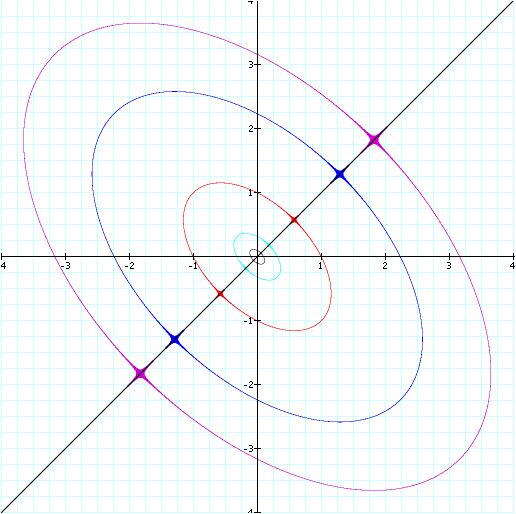
Larger equivalent subtrahends result in larger ellipses intersecting both x and y axes at:

Decreasing equivalent subtrahends result in ellipses that decrease in size until n=0. When n ≤ 0, the ellipse disappears and the remaining graph is the line y = x.

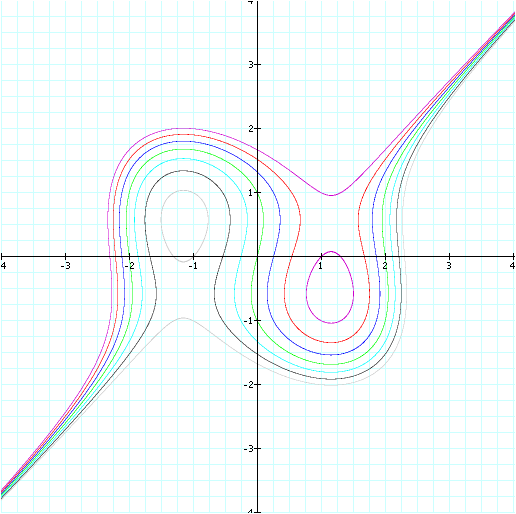
After exploring the original equation, the following graph is given

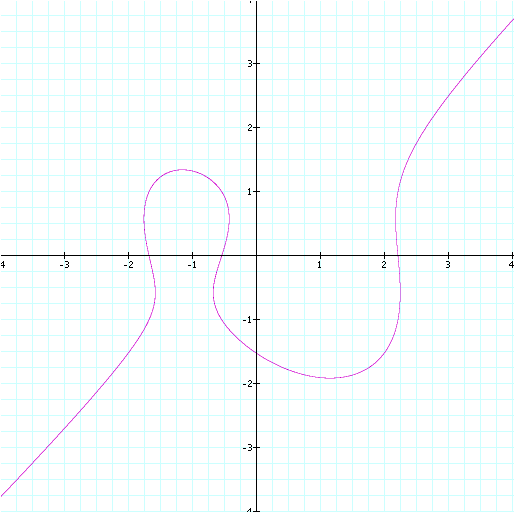
The graph above corresponds to the following equation:

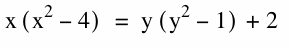
When a constant is added to one side of the equation, the shape of the graph changes.

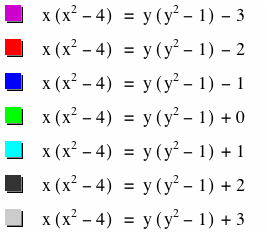
Here we added seven integers from -3 to 3. The resulting graph is below:

Finally we look at the following equation:

This is a three dimensional equation that yields the following graph:

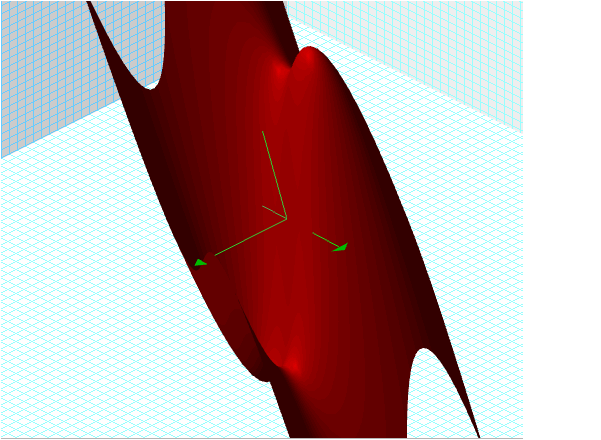
From looking at the three dimensional equation, we can see what happens when we vary the x-variable: