http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/EMAT6680.gif

Rayen Antillanca. Assignment 3

 

The general form of quadratic equation is: . We are interested in exploring how the parameter b affects the roots of this equation.

First Investigation

 

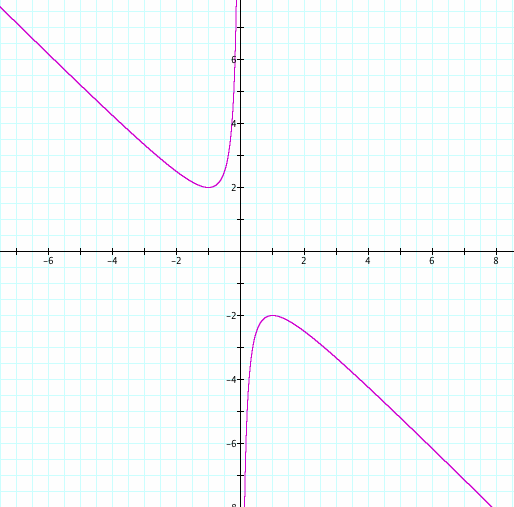
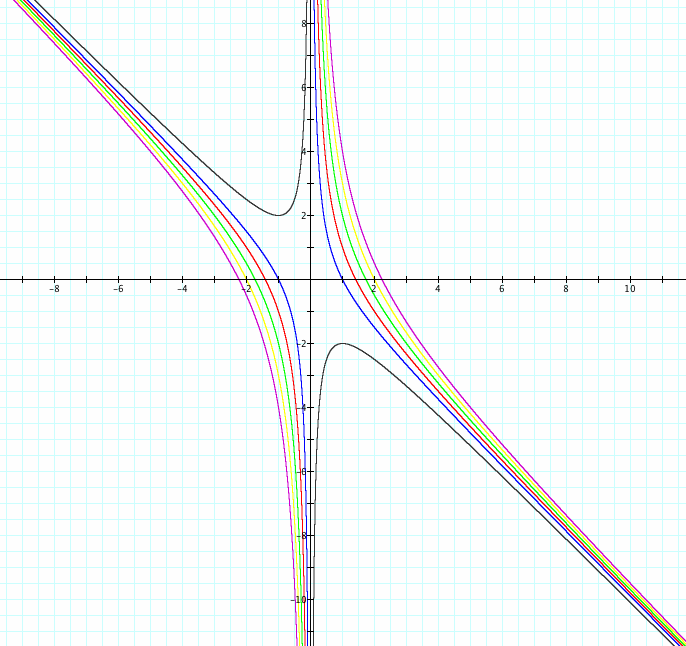
I am going to consider the equation . To explore the effect of parameter b on the roots, I will solve the equation  for b, so that I can plot the relationship between the roots and b on the xb plane. Solving for b gives us  whose graph is shown in figure 1.

 

 

This graph shows the relation between x and b

The purple curve is a hyperbola with vertical asymptote  and with a diagonal asymptote given by

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment3/g2.gif

Figure 1

 

 

 

If we fix the value of b, for instance b=4, there will be two values for x represented by the intersection of b = 4 and the red curve. These values of x coincide with the roots of the equation .

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment3/g4.gif

 

Summary

Different values of b are represented by the horizontal purple line above. Varying b implicates to move horizontally the purple line, and the number of intersections of this line with the red curve represent the number and the location of the roots for . In other words, if b>2 we get 2 real negatives roots if b=2 we get one negative root; when -2<b<2 we get no real roots, when b=-2 we get one positive root n when b<-2 we get two real roots

 

Second Investigation

 

Now, let’s see what happens when c=-1

 

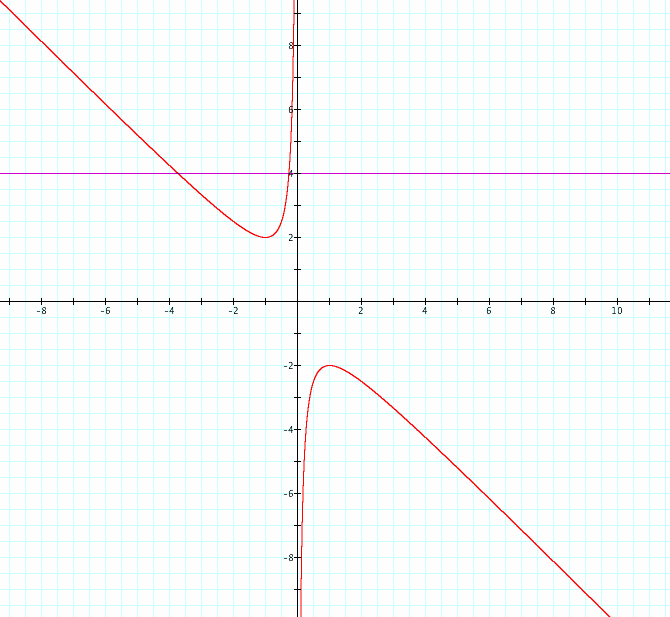
The next figure shows the graph of  for c=1 (purple curve) and c=-1 (blue curve).

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment3/g3.gif

As you can see, with c=-1 the new function is a hyperbola whose branches are in the first and third quadrant with asymptotes  and . When , regardless the value of b, we always get two intersections between the horizontal line and the blue curve. That is, the equation  has always two real roots (one positive and the other negative).

 

 

 

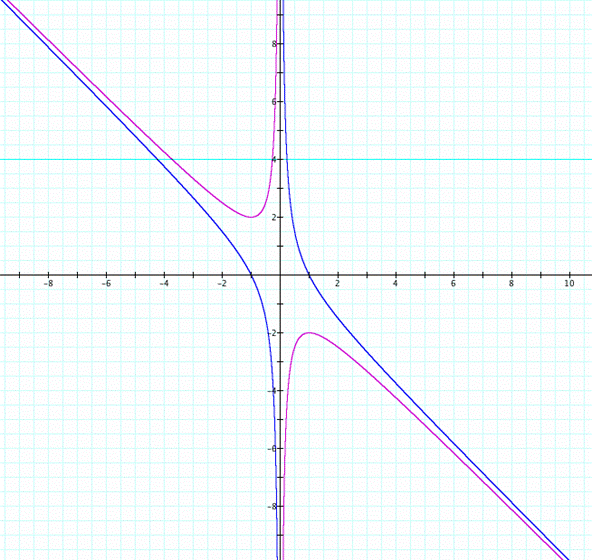
The next figure shows what happens with the graph of  as c < 0 varies.

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment3/eq2.gif

http://jwilson.coe.uga.edu/EMAT6680Fa11/Antillanca/Assignment3/g5.gif

 

 

Summary

We can observe that as long as c<0, the equation  has two real roots, regardless the value of b. When c<0, this gives a family of hyperbolas with one branch on the first and fourth quadrants, and the other one on the second and third quadrants. These hyperbolas have a vertical asymptote  and at diagonal asymptote given by .

 

 

Note: All graphs of this webpage were made with Graphing Calculator 4.0

 

 

Rayen's Homepage