EMT 668 - Algorithms & Computers
ASSIGNMENT 1, #5

Kimberly N. Bennekin

PROBLEM: Examine the graphs of y = a sin (bx + c) for different values of a, b & c.

y = sin (x + 1)

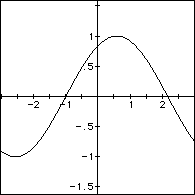
In order to examine other sine graphs, I will vary a, b and c individually and discuss the results. I will begin with a, by substituting 2, 3, -1, -2, and -1/2.

y = 2 sin(x+1) - red
y = 3 sin(x+1) - green
y = - sin(x+1) - blue
y= -2sin(x+1) - brown
y = -1/2sin(x+1) - purple

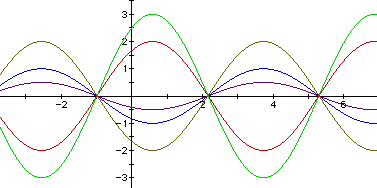
The graphs indicate that the numeric value of a will affect the height of the sine wave. For a=2, the sine wave increases to 2 and decreases to -2. For a=3, it increases to 3 and decreases to -3, and so on. If a is negative, this creates a reflection about the x-axis. By definition, a is the amplitude of y = a sin (bx + c).

I will do the same to b, by substituting 2, 3, 1/2, -1 and -2.

y = sin (2x+1) - red
y = sin (3x+1) - green
y = sin(1/2x+1) - blue
y = sin(-x+1) - brown
y = sin(-2x+1) - purple

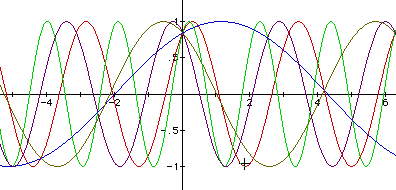
Changing b increases the intensity of the sine wave. By restricting the domain of our graph to [-pi,pi], we notice that as b increases, we increase the number of complete waves within this region. As b decreases (as in y = sin(1/2x+1)), we decrease the number of complete waves within this region. This happens because b directly affects the period of the sine wave. The period of a trigonometric function is the distance of one complete wave. The sign of b shifts the graph horizontally. This brings us to c . I will substitute 2, 3, -1, and -1/2 for c.

y = sin(x+2) - red
y = sin(x+3) - green
y = sin(x+(-1)) - blue
y = sin(x+(-1/2)) - brown

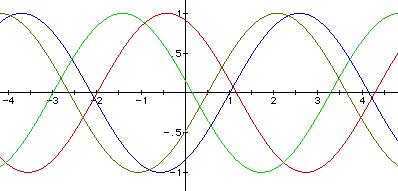
The value of c yields a horizontal phase shift of the graph. If c is positive, the graph shifts c units to the left. If c is negative, the graph shifts c units to the right. Recall, y = sin(-x+1) gave us a horizontal shift (by substituting b= -1) to the right. This happened since y = sin (-x+1) is equivalent to y = sin - (x - 1), written in standard form. This allows us to see that c = -1. This is why we have a shift to the right 1 unit.